مجموع دو پاره خط خواسته شده را محاسبه کنید

Question

در مربع ABCD از راس A به ضلع CD خطی دلخواه رسم می‌کنیم نقطه برخورد خط با ضلع CD را E می نامیم نیمساز زاویه تشکیل شده بین دو خط AE و AB را رسم می‌کنیم محل برخورد نیمساز با ضلع BC را M می نامیم در این صورت مجموع BM و DE کدام است؟

Answer 1

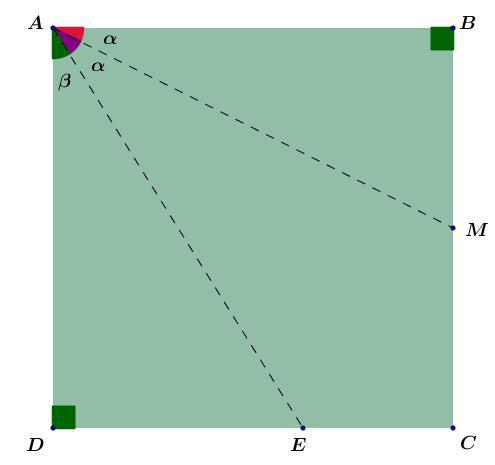
مثلث $ \triangle AED , \triangle ABM $ رو در نظر بگیرید از داشته های مثلثاتی استفاده میکنیم :

$$\tan \beta =\dfrac{DE}{AD}\ \ \ \ \tan \alpha =\dfrac{BM}{AB} \tag{1}$$

میدانیم که :

$$ \beta +2 \alpha =90^ \circ $$ $$\tan \beta=\tan (90^ \circ -2 \alpha )=\cot 2 \alpha $$

حال رابطه $(1)$ را با هم جمع میکنیم :

$$\cot 2 \alpha +\tan \alpha =\dfrac{DE}{AD}+\dfrac{BM}{AD}=\dfrac{DE+BM}{AD}$$

$$\cot 2 \alpha +\tan \alpha =\dfrac{1}{\sin 2 \alpha }$$ $$DE+BM=\dfrac{AD}{\sin (2 \alpha )}$$

Answer 2

enter link description here

طول ضلع مربع را$a$فرض کنیم و$ \alpha =\angle DEA $

$l+m= \frac{a}{tan \alpha }+a \times tan\frac{ \alpha }{2} $

$a[\frac{1- tan^{2}(\frac{\alpha }{2}) }{2tan \frac{ \alpha }{2}}+tan \frac{\alpha }{2}] $=

$ a[ \frac{1+tan^{2}(\frac{ \alpha }{2}) }{2tan \frac{ \alpha }{2} }] $=

$ \frac{a}{sin \alpha} $=

باتوجه به اینکه

$ \frac{\pi }{4}<\alpha<\frac{ \pi }{2} \Rightarrow a<l+m=\frac{a}{sin \alpha}< \sqrt{2} $</math,