ثابت کنید اندازه پاره خط DE با مجموع اندازه های AD و BE برابر است.

Question

در مثلث ABC نیمساز زاویه های A و B یکدیگر را در نقطه O قطع کرده اند. ثابت کنید اگر از نقطه O خطی موازی با AB رسم شود و ضلع های AC و BC را به ترتیب در D و E قطع کند، آنگاه اندازه پاره خط DE با مجموع اندازه های AD و BE برابر است.

Comments

سلام حل این سوال ساده است . اگر شکل را رسم کنید و خط موازی آن را بکشید یعنی خط ED که موازی با AB است ،می توان به راحتی ثابت کرد که دو مثلثODCوOBEمتساوی الساقین است،که مسئله حل شده خواهد بود.

Answer 1

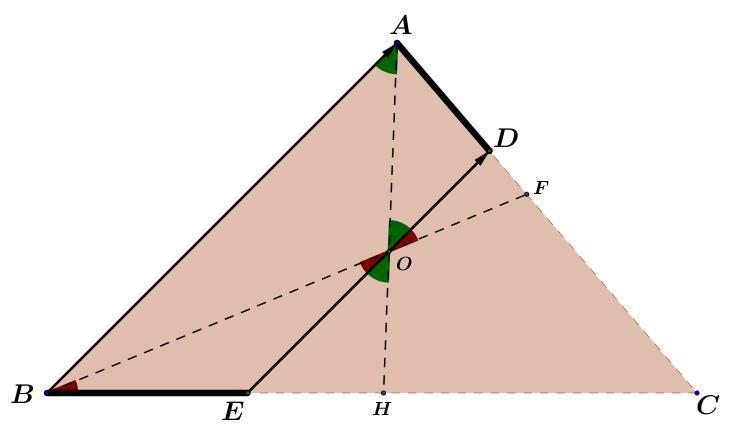
شکل رو در نظر بگیرید باتوجه به خطوط موازی مورب خواهیم داشت :

$$ \angle BOE = \angle \dfrac{B}{2}\ \ \ \ \ , \ \ \ \ \angle DOA = \angle \dfrac{A}{2} \tag{1}$$ از $(1)$ نتیجه میگیریم که دو مثلث $ \triangle BOE , \triangle AOD$ مثلث متساوی الساقین هستند نتیجه میگیریم :

$$AD=OD ,BE=OE$$

بنابراین اثبات کردیک که :

$$DE=OE+OD =AD+AD$$ $\Box .$