چون شرط خاصی روی تابعتان نگذاشتهاید و تنها چیزی که میخواهید این است که در تعداد متناهی نقطه مقدار دادهشدهای را اتخاذ کند میتوانید از درونیابیهای چندجملهای که در درس آنالیز عددی ۱ گفته میشوند استفاده کنید. پیاده کردن یک الگوریتم برای یافتن چنین چندجملهایهایی بسیار سادهاست و میتوانید با هر زبان برنامهنویسیای خودتان آن را انجام دهید. نرمافزارهای ریاضی مانند Matleb، Maple، Mathematica و SageMath هم دستورهای آماده برای این مورد دارند. چون نام Matlab را آوردید، من هم برایتان دستور Matlab را اشاره میکنم. نخست بردار مقدار $x$هایتان را میدهید و آن را نامگذاری میکنید مثلا points_x و سپس بردار $y$هایتان را متناسب به ترتیب بردار $x$هایتان میدهید و آن را نامگذاری میکنید مثلا points_y. برای نمونه فرض کنید نقطههایمان اعضای مجموعهٔ زیر هستند
$$\{(-1,5),(0,0),(\frac{1}{2},5),(2,3),(2.1,-1),(2.5,1)\}$$
پس خطهای اولیهٔ کد Matlabمان میشوند:
points_x=[-1,0,1/2,2,2.1,2.5];
points_y=[5,0,5,3,-1,1];
اکنون توجه کنید که برای اینکه مطمئن شوید چندجملهای که درونیابی میکنید حتما از $n$ دادهتان بگذرد باید درجهٔ چندجملهای دستکم $n-1$ باشد. چون در این مثال ۶ نقطه داریم پس درجه باید دستکم ۵ باشد. دستور مربوطه polyfit است (نام آن نشاندهندهٔ fit کردن یک polynomial است). این دستور سه ورودی دارد، بردار $x$ها، بردار $y$ها و درجهٔ چندجملهای که میخواهید. پس دستور بعدی ما میشود
p=polyfit(points_x,points_y,5)
کاری که Matlab خواهد کرد این است که ضرایب این چندجملهای را محاسبه و سپس ضریب جملهٔ با توان بزرگتر به ضریب جملهٔ با توان کوچکتر به ترتیب در یک بردار قرار میدهد با نامی که برایش تعیین کردهاید. اینجا این نام را p گذاشتهایم. توجه کنید که اگر در انتهای دستوری از ; استفاده کنید آنگاه خروجی آن خط نمایش داده نمیشود و برای همین در انتخای خط سوم این علامت را نگذاشتیم. حاصل برابر است با:

پس چندجملهایِ محسابه شده برابر است با
$$f(x)=(7.8612)x^5-(29.4577)x^4+(9.4846)x^3+(41.7488)x^2-(10.0547)x$$
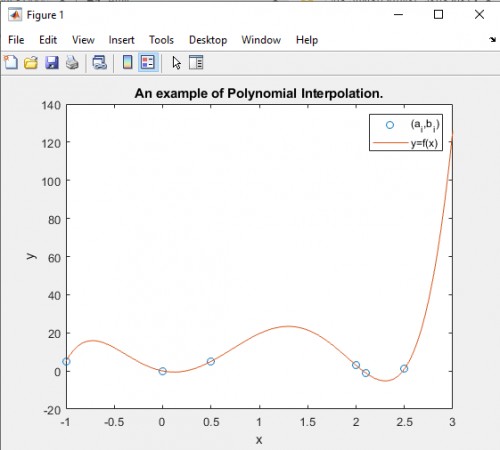
است (جملهٔ ثابت صفر بودهاست که نوشتنش فرقی ایجاد نمیکند). در زیر رسم نمودار این تابع به همراه ۶ نقطه توسط همان نرمافزار Matlab نیز آوردهشدهاست که میتوانید به صورت بصری نیز ببینید که تابع یافتشده از همهٔ نقاط خواستهشده میگذرد.