پاسخ شما خیر است. تابع زیر را در نظر بگیرید.
$$f(x)=\begin{cases}
x\sin(\frac{1}{x}) & ;\;x\neq 0\\
0 & ;\;x=0
\end{cases}$$
این تابع بر روی کل $\mathbb{R}$ تعریف شدهاست. نمودار این تابع را در زیر میبینید.
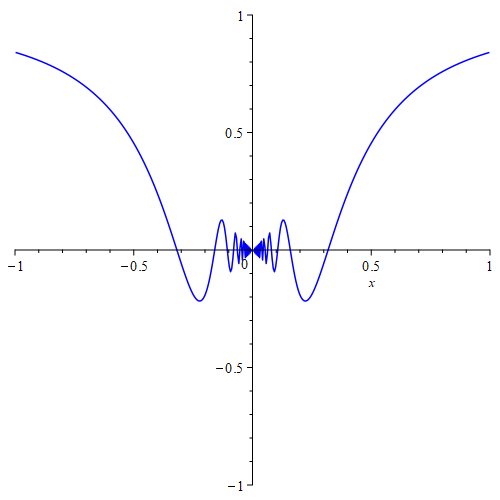
اکنون بیایید این تابع را بر روی بازهٔ $[0,\frac{1}{2}]$ در نظر بگیریم. نقطهٔ $x=0$ نقطهٔ شروع این بازه است ولی آیا یک کمینه یا بیشینه نیز است؟ خیر، چون هر همسایگیِ راستی از این نقطه بردارید، هر چقدر هم که کوچک باشد، دارای دو نقطه هست که مقدار تابع در یکی از آنها منفی و در دیگری مثبت شود، پس هرگز یک همسایگی راست از این نقطه نمیتوانید پیدا کنید که مقدار تابع در صفر که صفر است از مقدار تابع بر روی کل این همسایگی فقط بیشتر یا فقط کمتر باشد. پس این نقطه نه کمینه است و نه بیشینه. توجه کنید که اکسترمم از واژهٔ نافارسیِ extrema به منظور نهایتِ پائین و بالا (مقدار تابع نه دامنهٔ تابع) میآید که همان کمینهها و بیشینههای نسبی هستند ولی چون $x=0$ این چنین نیست، پس اکسترمم نمیباشد. نمودار تابع در بازهٔ یادشده را در زیر میبینید.
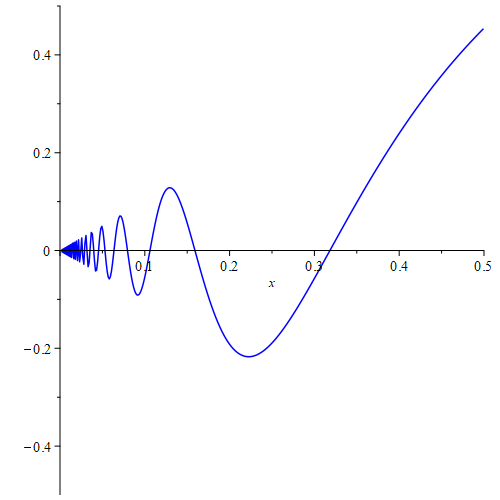
به روش مشابه میتوانید با بازهٔ $[-\frac{1}{2},0]$ ببینید که نقطهٔ پایانیِ یک بازه نیز الزاما اکسترمم نیست.