به نام خدا.
در شکل زیر $S$ نشان دهنده فضای نمونه است و $x_k$ که اگر $k$ زوج باشد به معنای احتمال خارج شدن توپ قرمز و اگر فرد باشد به معنای خارج کردن توپ آبی است. $p_i$ به معنای احتمال خارج کردن توپ قرمز از فضای نمونه $S_i$ است. می توان نشان داد که اگر یک مهره بدون دانستن رنگ آن خارج کنیم، احتمال اینکه مهره دوم قرمز باشد برابر است با احتمال قرمز بودن مهره اول.
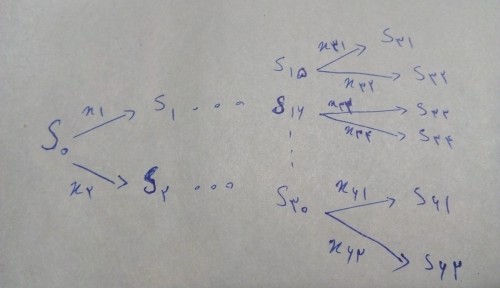
حال فرض میکنیم که برای خارج کردن $4$ توپ نیز احتمال تغییر نمی کند. نشان می دهیم که برای $5$ توپ نیز تغییری ایجاد نخواهد شد.
پس از اینکه چهارمین مهره را خارج کنیم، ما $16$ تا فضای نمونه داریم. که آنها را
$S_{15} ,\space S_{16},...,S_{30}$
می نامیم. حال مهره پنجم را خارج می کنیم. $32$ فضای نمونه داریم. که می نامیم:
$S_{31}, \space S_{32},...,S_{62}$
می دانیم که طبق فرض استقرا با خارج کردن چهار مهره احتمال قرمز بودن مهره پنجم برابر است با احتمال قرمز بودن مهره اول . کافیست در قانون احتمال کل که برای $4$ توپ نوشتیم، قرار دهیم:
$p_{15}=x_{31}×p_{31}+x_{32}×p_{32}$
$p_{16}=x_{33}p_{33}+x_{34}p_{34}$
.
.
.
$p_{30}=x_{61}S_{61}+x_{62}S_{62}$
یعنی برای هر $p_j$ که
$15 \leq j \leq 30$
عبارت مساوی آن را قرار دهیم. پس به این نتیجه خواهیم رسید که برای خارج کردن $5$ توپ نیز احتمال تغییری نخواهد کرد.