حاصل $\lim_{x\to 0^+}\frac{\lfloor x\rfloor}{\lfloor x\rfloor}$ چیست؟
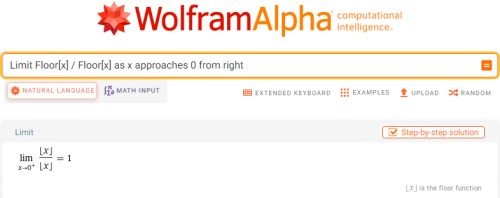
دامنۀ تابع $f(x) = \frac{\lfloor x\rfloor}{\lfloor x\rfloor}$ برابر با $\mathbb{R}-[0, 1)$ است. اگر بخواهیم حد راست این تابع را در نقطۀ $x = 0$ بهدست بیاوریم، ابتدا باید توجه کنیم که این تابع باید در یک همسایگی راست $x = 0$ (مانند $(0, 1)$) تعریف شده باشد، ولی میبینید که با توجه به دامنۀ تابع، اینگونه نیست. پس حد راست تابع در این نقطه، موجود نیست. اما نرمافزار Wolfram Mathematica، عدد 1 را در خروجی نمایش میدهد:

همانطور که میبینید، حاصل این حد را با استفاده از دستور Limit، در این نرمافزار محاسبه کردهام و نرمافزار در خروجی عدد 1 را نمایش دادهاست. در حالی که گفتیم که اصلاً تابع در این نقطه حد راست ندارد! آیا نرمافزار در حال انجام اشتباهی است؟ البته در وبگاه WolframAlpha نیز دقیقاً همین خروجی را نمایش میدهد. مشکل از کجاست؟