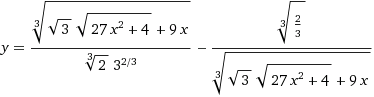با تعویض نقش $x$ و $y$ داریم $y^3+y-x=0$ .در اینصورت کافی است که این معادله را حل کنیم.
برای دیدن روش های حل معادله درجه سوم میتونید اینجا رو ببینید: تابع درجه سوم
در واقع برای حل معادله درجه سوم $ax^3+bx^2+cx+d=0$ میتونیم با تقسیم طرفین بر $a$ و قرار دادن $x=t-\frac b{3a}$ آن را به معادله به صورت $ t^3+pt+q=0 $ تبدیل کرد که $p=\frac{3ac-b^2}{3a^2}$ و $q=\frac{2b^3-9abc+27a^2d}{27a^3}$ . سپس دو متغیر $u,v$ را در نظر میگیریم که در $t=u+v$ صدق می کنند. در اینصورت می توان ثابت کرد
$u=\sqrt[3]{-\frac q2+\sqrt{\frac{q^2}4+\frac{p^3}{27}}}$ و $v=\sqrt[3]{-\frac q2+\sqrt{\frac{q^2}4+\frac{p^3}{27}}}$
در صورتی که زیر رادیکال های با فرجه زوج مثبت باشد در اینصورت جواب حقیقی خواهیم داشت.
با استفاده از این روش خواهید توانست معادله خواسته شده مساله را حل کنید.
من با wolframalpha حل کردم میتونید جواب رو در اینجا ببینید: کلیک کنید!