فضای اندازه پذیر
فرض کنید که $X$ یک مجموعه نا تهی باشد و $\Sigma$ مجموعه ایی از زیر مجموعه های $X$ باشد . میگوییم $ \Sigma$ یک سیگما جبر از زیر مجموعه های $X$ است اگر شرایط زیر را داشته باشد.
وجود داشته باشد حداقل $A \subseteq X $ به طوری که $ A \in \Sigma $.
اگر $A \in \Sigma $ آنگاه $A^c \in \Sigma$ که $A^c=X \backslash A$.
اگر $A_n \in \Sigma$ برای همه $n\in \mathbb{N}$ آنگاه $ \bigcup_{n=1} ^{\infty}A_n \in \Sigma$.
جفت مرتب $(X,\Sigma)$ را فضای اندازه پذیر گوییم.
تعریف احتمال
اگر $(X,\Sigma)$ فضای اندازه پذیر باشد و تابع اندازه
$ P:\Sigma \to \mathbb{R} $
به طوری باشد که.
اگر $P(X)=1$.
برای هر $E \in \Sigma $ داشته باشیم $P(E) \geq 0$.
داشته باشیم $P( \bigcup_{n=1}^{ \infty } E_{n} )= \sum_{n=1}^{ \infty } P( E_{i} )$ با شرط اینکه $E_n \in \Sigma$ برای همه ی $n\in \mathbb{N}$ داشته باشیم $E_i \cap E_j \neq \emptyset : \ \ i,j \in \mathbb{N} ,i\neq j$.
آنگاه به سه تایی مرتب $(X,\Sigma ,P)$ فضای احتمال گوییم.
قوانین احتمال
اگر پیشامد های $E_1,E_2,E_3,...,E_k$ پیشامد های دو به دو مجزا یعنی $E_i \cap E_j \neq\emptyset \ : \ i\neq j ,i,j \in \mathbb{N}$ آنگاه خواهیم داشت.
$${\bbox[5px ,border:1px solid #4682B4]{P( \bigcup_{k=1}^{ n } E_{n} )= \sum_{i=1}^{ n } P( E_{i} )
}} $$
برای هر دو پیشامد دلخواه ( الزامی ندارد دو به دو مجزا باشند ) $ A,B \in \Sigma $ داریم.
$${\bbox[5px ,border:1px solid #4682B4]{P(A\cup B)=P(A)+P(B)-P(A\cap B)}}$$
برای دو پیشامد دلخواه
$A,B \in \Sigma$
داریم.
$${\bbox[5px ,border:1px solid #4682B4]{P(A-B)=P(A)-P(A\cap B)}} $$
که اگر $A \subset B$ باشد آنگاه $A\cap B =B$ در نتیجه رابطه به صورت زیر است
$${\bbox[5px ,border:1px solid #4682B4]{P(A-B)=P(A)-P(B)}} $$
که با توجه به اینکه $P(A-B)\geq 0$ خواهیم داشت
$P(A) \geq P(B)$.
میدانیم که هر مجموعه از $\Sigma$ زیر مجموعه مجموعه $X$ است . در نتیجه مجموعه دلخواه $A$ در نظر بگیریم خواهیم داشت $A \subset X$ در نتیجه $0\leq P(A) \leq P(X)=1$ در نتیجه احتمال یک پیشامد عددی در بازه ی $[0,1]$ است . که احتمال پیشامد وقتی صفر است که مجموعه $A$ تهی باشد زیرا $\emptyset \cap \emptyset \neq 0$ و همچنین $\emptyset \cup \emptyset =\emptyset$ خواهیم داشت.
$${\bbox[5px ,border:1px solid #4682B4]{P(\emptyset)=P(\emptyset)+P(\emptyset) \Longrightarrow P(\emptyset)=0
}} $$
اگر پیشامد $A^c$ متمم پیشامد $A$ باشد آنگاه داریم.
$${\bbox[5px ,border:1px solid #4682B4]{P(A)=1-P(A^c)
}} $$
احتمال در فضای همشانس و شمارای متناهی
فرض کنید که مجموعه $X$ متناهی باشد یعنی به صورت
$X=\{ e_1,e_2,e_3,...,e_n \}$ و مجموعه $\Sigma $ برابر مجموعه تمام زیر مجموعه های مجموعه $X$ باشد . در این صورت مجموعه $\Sigma$ سیگما جبر از زیر مجموعه های $X$ است . اعداد مثبت $p_1,p_2,p_3,....,p_n$ را که مجموعه آنها برابر یک است یعنی $p_1+p_2+p_3+....+p_n=1$ را در نظر میگیریم . و برای هر مجموعه $ E \in \Sigma$ داشته باشیم.
$$P(E)= \sum_{e_i \in E} P_i$$
در این صورت تابع $P:\Sigma \to \mathbb{R}$ تابع اندازه است و سه تایی مرتب $(X,\Sigma ,P)$ فضای احتمال است. با توجه به تعریف خواهیم داشت.
$$\bbox[5px ,border:1px solid #4682B4]{P(\{e_i\})=P(e_i)=p_1 \ \ \ \ : \ \ i =1,2,..,n }$$
گوییم فضا همشانس است به طوری که داشته باشیم $p_1=p_2=p_3=...=p_n=\dfrac{1}{n}$ در این صورت احتمال هر مجموعه به صورت $ \{e_1\}$ برابر است با.
$$\bbox[5px ,border:1px solid #4682B4]{P(\{e_i\})=P(e_1)=p_1=\dfrac{1}{n}
}$$
اگر $n(A)$ تعداد عضو های پیشامد $E$ باشد و $n(S)$ تعداد عضوی های فضای نمونه ای باشد آنگاه احتمال پیشامد $E$ در فضای همشانس خواهد بود.
$${\bbox[5px ,border:1px solid #4682B4]{P(A)=\dfrac{n(A)}{n(S)}
}}$$
قانون ضرب احتمال
فرض کنید که سه تایی $(X,\Sigma,P)$ یک فضای احتمال باشد و $B\in\Sigma$ به طوری که $P(B)>0$ . حال تابع اندازه دیگری را به صورت زیر تعریف میکنیم .
$$P_B(A)=P(A \mid B):=\dfrac{P(A \cap B)}{P(B)}$$
$P_B(A)=P(A \mid B)$ به این معنی است که احتمال پیشامد $A$ با علم به اینکه پیشامد $B$ اتفاق افتاده است .
در این صورت میتوان ثابت کرد که سه تایی $(X,\Sigma,P_B)$ یک فضای احتمال است . این فضای احتمال را فضای احتمال شرطی گوییم .
اگر $A,B$ دو پیشامد دلخواه باشند آنگاه با توجه به فضای احتمال شرطی خواهیم داشت.
$${\bbox[5px ,border:1px solid #4682B4]{P(A \cap B)=P_B(A)P(B)}} $$
که به این رابطه قانون ضرب احتمال گوییم.
افراز یک مجموعه
فرض کنید $A$ یک مجموعه دلخواه باشد . آنگاه $S$ مجموعه ای از زیر مجموعه های $ A_1,A_2,A_3,...,A_n$ مجموعه $A$ باشد به طوری شرایط زیر را داشته باشد .
مجموعه تهی عضو مجموعه $S$ نباشد به این معنی که
$\emptyset \notin S $.
و همچنین $A_j\cap A_i =\emptyset \ \ \ : \ \ 0\leq i\neq j \leq n $.
و در آخر $ \bigcup_{i=1}^n A_i=S $.
آنگاه گوییم مجموعه $S$ یک افراز برای مجموعه $A$ است.
قانون احتمال مرکب و فرمول بیز
$ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ $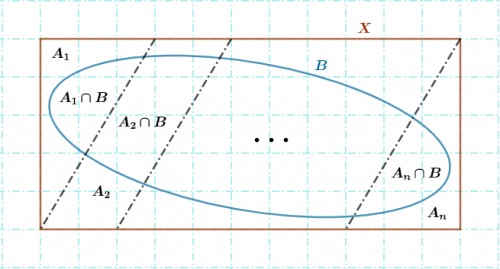
فرض کنید که سه تایی $(X,\Sigma,P)$ یک فضای احتمال باشد و $A_1,A_2,A_3,...,A_n$ پیشامد هایی از این فضای احتمال باشد به طوری که مجموعه
$C=\{A_1,A_2,A_3,...,A_n\}$ یک افراز برای مجموعه $X$ باشد . و همچنین $B$ پیشامد دلخواه دیگری از این فضای احتمال باشد به طوری که $P(B)\neq 0$ باشد خواهیم داشت .
$$B=B \cap X =B\cap(\bigcup_{i=1}^n A_i)=\bigcup_{i=1}^n (B\cap A_i)$$
در این صورت ثابت میشود که مجموعه $$C=\{(B\cap A_1),(B\cap A_1),(B\cap A_2),(B\cap A_1),...,(B\cap A_n)\}$$ یک افراز برای مجموعه $B$ است در نتیجه با توجه به اصل احتمال و قانون ضرب احتمالات خواهیم داشت.
$$
\begin{align}P(B)&=\sum_{i=1}^nP(B \cap A_i)
\\ &=\sum_{i=1}^n P(B\mid A_i)P(A_i)
\\ &=\sum_{i=1}^n P_ {A_i}(B)P(A_i)
\end{align}$$
که به این رابطه قانون احتمال مرکب گوییم. از قانون ضرب احتمال میدانیم که.
$$P(B \cap A_i)=P(B\mid A_i)P(A_i)$$
$$P(A_i \cap B)=P(A_i\mid B)P(B)$$.
میدانیم که احتمال این دو برابر هستند در نتیجه خواهیم داشت.
$$P(A_i \cap B)=\dfrac{P(B\mid A_i)P(A_i)}{P(B)}$$.
و با استفاده از قانون احتمال مرکب خواهیم داشت.
$${\bbox[5px ,border:1px solid #4682B4]{P(A_i \cap B)=\dfrac{P(B\mid A_i)P(A_i)}{\sum_{i=1}^n P(B\mid A_i)P(A_i)}}}$$.
این رابطه به فرمول بیز معروف است .
پیشامد مستقل
فرض کنید که سه تایی $(X,\Sigma,P)$ یک فضای احتمال باشد و $B\in\Sigma$ به طوری که
$P(B) > 0$ و $A$
پیشامد دلخواهی در این فضای احتمال باشد و همچنین داشته باشیم.
$$P(A\mid B)=P(A)$$
آنگاه گوییم پیشامد $A$ مستقل از پیشامد $ B$ است. و همچنین اگر
$P(A) > 0$ باشد پیشامد $B$ مستقل از پیشامد $A$ است.
در نتیجه اگر دو پیشامد دلخواه با $P(A) > 0 , P(B) > 0$ و مستقل از یکدیگر باشند خواهیم داشت.
$${\bbox[5px ,border:1px solid #4682B4]{P(A\cap B)=P(A)P(B)}}$$
منابع
آمار و احتمال مقدماتی جواد بهبودیان
آمار و احتمال شلدون راس
$\text{Measure Theory .M.Papadimitrakis}$
صادق صادری مهران