مجموعه کانتور:
در این مطلب به معرفی مجموعه کانتور که اهمیت خاصی در آنالیز ریاضی داره می پردازیم.
شاید اگر از ما سوال بشه که مجموعه ای کامل(مجموعه بسته ناتهی که نقطه ایزوله ندارد) در اعداد حقیقی مثال بزنید تنها مثال هایی که به ذهن بیان بازه های بسته یا حداکثر اجتماع متناهی از بازه های بسته باشند. همینطور پیدا کردن مجموعه ای کامل در اعداد حقیقی که هیچ جا چگال باشد( $A\subset\mathbb R$ را هیچ جا چگال گوییم هرگاه $ \overline{A}^ \circ =\emptyset $ ) شاید ساده نباشد. در اینجا میخواهیم همچین مجموعه ای را معرفی کنیم.
ساخت مجموعه کانتور:
بازه $=[0,1]$ را در نظر می گیریم و از آن یک مجموعه چگال باز $G$ را (به ترتیبی که در ادامه توضیح داده خواهد شد) جدا می کنیم. در اینصورت مجموعه ای که باقی می ماند $K=[0, 1]\setminus G$ یک مجموعه بسته ی هیچ جا چگال در بازه بسته صفر و یک خواهد بود.
بازه $=[0,1]$ را به سه قسمت مساوی تقسیم می کنیم:
$$\qquad [0, \frac13]\quad [\frac 13, \frac 23]\quad[\frac 23, 1]$$
با کنارگذاشتن بازه یک سوم میانی $G_1=(\frac 13, \frac 23)$بازه های زیر باقی می مانند:
$$K_1:\qquad [1, \frac 13]\qquad [\frac 23, 1]$$
به عبارت دیگر $K_1=[0, 1]\setminus G_1$
حال همین کار را روی هر کدام از بازه های جدید تکرار می کنیم یعنی بازه های یک سوم میانی آنها که $(\frac 19, \frac 29)$ و $(\frac 79, \frac 89)$ هستند را کنار می گذاریم. در اینصورت داریم:
$$K_2:\quad [0, \frac 19]\ [\frac 29, \frac 39]\qquad [\frac 69, \frac 79]\ [\frac 89, 1]$$
اگر $G_2=(\frac 19, \frac 29)\cup(\frac 79, \frac 89)$ در اینصورت $K_2=[0, 1]\setminus (G_1\cup G_2)$
چنانچه همین روند را ادامه دهیم به دنباله های $\{K_n\}$ و $\{G_n\}$ می رسیم که دارای ویژگی های زیر هستند:
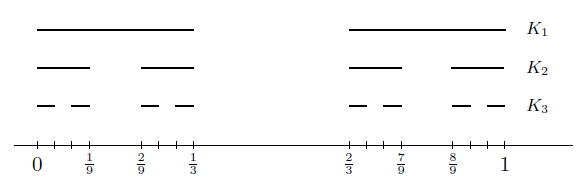
- مجموعه $G_n$ به صورت اجتماع دو به دو مجزای $2^{n-1}$ بازه باز به طول $(\frac 13)^n$ است.
- مجموعه $K_n$ به صورت اجتماع دو به دو مجزای $2^n$ بازه بسته به طول $(\frac 13)^n$ است.
- برای هر $n$ داریم $$K_n=[0, 1]\setminus (G_1\cup\cdots G_n)$$
در اینصورت مجموعه کانتور که با $K$ نمایش می دهیم برابر است با: $$\color{red}{K=\bigcap_1^\infty K_n}$$
اگر قرار دهیم $$G=\bigcup_1^\infty G_n$$ در اینصورت واضح است که $$K=[0, 1]\setminus G$$
از انجا که $K_n$ ها مجموعه هایی بسته هستند و اشتراک شمارا از مجموعه های بسته مجموعه ای بسته است لذا
- مجموعه کانتور $K=\bigcap_1^\infty K_n$ مجموعه ای بسته است.
بنابر مورد 1 که ذکر شد هر $G_n$ دارای $2^{n-1}$ مولفه به طول $(\frac 13)^n$ است بنابراین طول هر $G_n$ برابر است با
$$2^{n-1}(\frac 13)^n=\frac 12(\frac 23)^n$$
و چون $G=\bigcup_1^\infty G_n$ بنابراین طول $G$ برابر است با
$$\sum_1^\infty \frac 12(\frac 23)^n=1$$
اما چون مجموعه کانتور $K=[0, 1]\setminus G$ بنابراین
- طول مجموعه کانتور برابر صفر است.
حال به سادگی می توان نتیجه گرفت که مجموعه کانتور هیچ جا چگال است، زیرا مجموعه کانتور بسته است و اگر قرار باشد $K^\circ\emptyset$ یعنی نقطه درونی مثل $a$ داشته باشد در اینصورت عددحقیقی مثبت $r$ موجود است که $(a-r, a+r)\subset K$ و این یعنی مجموعه کانتور شامل بازه ای به طول مثبت است در حالیکه ثابت کرده ما ثابت کردیم طول مجموعه کانتور صفر است. پس ثابت شد
- مجموعه کانتور هیچ جا چگال است.
- درون مجموعه کانتور تهی است.
برای اثبات کامل بودن مجموعه کانتور باید نشان دهیم هیچ نقطه ای از آن ایزوله نیست. فرض کنید $a\in K$ و $r> 0$ دلخواه باشد باید ثابت کنیم $b\in K$ موجود است که $0< |a-b|< r$ . عدد طبیعی $n$ را چنان انتخاب کنید که $\frac 1{3^n}< r$ . اما چون $a\in K$ پس $a\in K_n$ فرض کنید $L$ آن مولفه از $K_n$ باشد که $a\in L$ . اما در ساخت مجموعه کانتور وقتی یک سوم میانی این مولفه $L$ را بر می داریم دو مولفه برای $K_{n+1}$ متناظر با این مولفه ایجاد می شود که آنها را $L_0$ و $L_1$ می نامیم. هر کدام از این مولفه ها دارای نقاطی از $K$ هستند. اگر مثلا $a\in L_0$ در اینصورت $ b$ را هر عضو دلخواه در $K\cap L_1$ در نظر بگیریم آنگاه $0< |a-b|< \frac 1{3^n}< r$ . یعنی ثابت کردیم
رویکرد عددی به ساخت مجموعه کانتور:
هر عدد حقیقی در مبنای سه را می توان به صورت $$a_na_{n-1}...a_1a_0.b_1b_2...$$
نمایش داد که $a_i, b_i$ ها $0$ یا $1$ یا $2$ هستند و بسط آن به صورت
$$a_n3^n+a_{n-1}3^{n-1}+...+a_13+a_0+b_1\frac 13+b_2\frac 1{3^2}+...$$
است. بنابراین هر عدد حقیقی ر بازه $(0, 1)$ به صورت $0.b_1b_2...$ خواهد بود. بسط اعشاری عدد حقیقی $a$در مبنای سه از الگوریتم زیر به دست می آید:
$$a\qquad i\qquad 3a\qquad b_i=\lfloor 2a \rfloor\qquad 2a-b_i$$
که $i$ مرحله $i$ ام را نشان می دهد. مثلا برای $\frac 18$ داریم:
$$\begin{array}{l|c|c|c|r}
a& i& 3a&b_i=\lfloor 3a\rfloor & 3a-b_i\\
\hline
\frac 18&1& \frac 38&0&\frac 38\\
\hline
\frac 38&2&\frac 98&1&\frac 18
\end{array}$$
بنابراین $b_1=0, b_2=1$ و چون باز به $\frac 18$ رسیدیم این الگوریتم دوباره تکرار می شود یعنی یک هشتم در مبنای سه برابر است با $$\frac 18=(0.\overline{01})_3=0.010101...$$
در ساخت مجموعه کانتور در مرحله اول که یک سوم میانی یعنی $(\frac 13, \frac 23)$ را کنار می گذاریم در واقع تمام اعدادی را که در بسط سه سه ای(در مبنای سه) آنها اولین رقم اعشار $1$ است را کنار گذاشتیم. زیرا اگر $\frac 13, a, \frac 23$ در اینصورت:
$$a \qquad 1\qquad \frac 3a\qquad b_1=\lfloor 3a\rfloor =1$$
یعنی تمام اعداد واقع در بازه $(\frac 13, \frac 23)$ دارای بسطی به صورت $0.1b_2b_3...$ در مبنای سه هستند.
و اگر به همین ترتیب بررسی کنید متوجه می شوید در مرحله دوم که بازه های یک سوم میانی را که برمیداریم در واقع اعدادی را کنار گذاشته ایم که در بسط اعشاری آنها در مبنای سه دومین رقم اعشار آن $1$ است.
پس مجموعه کانتور عبارت است از همه اعداد واقع در $[0, 1]$ که در نمایش اعشاری مبنای سه آنها رقم $1$ وجود ندارد.
که همین ثابت می کند
- مجموعه کانتور مجموعه ای ناشمارا است یعنی $card (K)=card(\mathbb R)=c$ .
اثبات این مطلب هم ساده است زیرا اگر تابع $f:K\to [0, 1]$ را به صورت
$$x=\sum_1^\infty \frac{b_i}{3^n}\to f(x)=\sum_1^\infty\frac{\frac{b_i}2}{2^n}$$
در نظر بگیریم از آنجا که $b_i$ ها فقط $0$ یا $2$ هستند پس $\frac{b_i}2$ یا صفر یا $1$ هستند یعنی نمایش اعشاری تمام اعداد در بازه ی $[0, 1]$ را در مبنای $2$ به دست می دهد. پس این تابع پوشا است لذا $card K\leq card\ [0, 1]$ و از طرفی چون $K\subset [0, 1]$ پس $card\ [0, 1]\leq card\ K$ .
البته اثبات ناشمارا بودن از کامل بودن مجموعه کانتور هم میشد نتیجه گرفت.
دیگر ویژگی های مجموعه کانتور
- مجموعه کانتور کلا ناهمبند است.
زیرا در غیر اینصورت باید شامل بازه ای باز باشد که ممکن نیست.
منابع:
The Elements of Real Analysis, Robert G. Bartle
Principles of Mathematical Analysis, Walter Rudin
Elementray Real Analysis S. Thomson& B. Bruckner& M. Bruckner
فضاهای متریک با طعم توپولوژی تالیف مجید میرزاوزیری
پ.ن1: لطفا اگر سوالی داشتید در قسمت پرسش سوال مطرح کنید. منتظر دیدگاه های ارزشمندتون هستم.
پ.ن2: مطالب مرتبط: تابع کانتور
نمایش از نو اسفند ۸, ۱۳۹۷