به نام خدا
فرمول هرون، فرمولی است که با استفاده از آن میتوان مساحت یک مثلث را فقط با داشتن طول اضلاع آن محاسبه کرد. این فرمول را میتوان برای هر نوع مثلثی بهکار برد. این فرمول را «هرون اسکندرانی» (Hero of Alexandria)، مهندس و ریاضیدان یونانی در 70-10 میلادی معرفی کرد. اگر طول سهضلع را با $a$، $b$ و $c$، مساحت را با $S$ و نصف محیط مثلث را هم با $p$ نمایشدهیم، این فرمول بهصورت زیر است:
$$S= \sqrt{p(p-a)(p-b)(p-c)}$$
اثبات فرمول هرون:
با استفاده از جبر و قوانین نسبتهای مثلثاتی میتوان این فرمول را اثبات کرد. این اثبات با اثباتی که هرون در کتابش (متریکا) در سال ۶۰ ق. م. منتشر کرده بود، کاملاً متفاوت است.
برای اثبات فرمول هرون، ابتدا مثلث زیر را در نظر بگیرید:
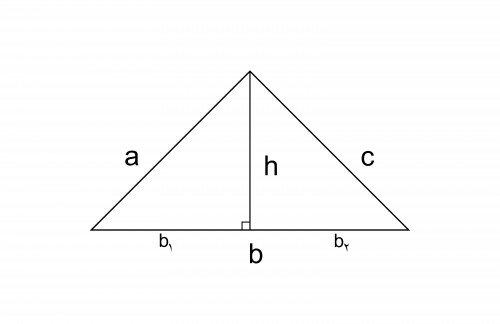
روابط زیر را دربارۀ این مثلث میتوان نوشت:
(1) $b_1+b_2=b$
(2) $b_1^2+h^2=a^2$
(3) $b_2^2+h^2=c^2$
دقتکنید که در روابط (2) و (3)، از قضیۀ فیثاغورس استفادهشدهاست.
خوب، حالا روابط (2) و (3) را از همدیگر کم میکنیم:
$$ \frac{{\begin{cases}b_1^2+h^2=a^2 & \\-(b_2^2+h^2=c^2) & \end{cases}}}{b_1^2-b_2^2=a^2-c^2 } $$
همانطور که دیدید، پس از اینکار، بهرابطۀ $b_1^2-b_2^2=a^2-c^2$ رسیدیم. با تجزیۀ سمتچپ این رابطه، این رابطه را بهصورت $(b_1-b_2)(b_1+b_2)=a^2-c^2$ میتوان نوشت. چون $(b_1+b_2)$ برابر با $b$ است، پس این رابطه را بهصورت زیر میتوان نوشت:
$$(b_1-b_2) \cdot b=a^2-c^2$$
در نتیجه:
$$b_1-b_2= \frac{a^2-c^2}{b} $$
حالا این رابطه را با رابطۀ $b_1+b_2=b$ جمع میکنیم:
$$ \frac{{\begin{cases}b_1-b_2= \frac{a^2-c^2}{b} & \\b_1+b_2=b & \end{cases}}}{b_1= \frac{a^2+b^2-c^2}{2b} } $$
که پس از اینکار به رابطۀ $b_1= \frac{a^2+b^2-c^2}{2b} $ میرسیم.
حالا رابطۀ (1) را که در ابتدای این اثبات بود در نظر بگیرید. با حل آن بر حسب $h$، به $h= \sqrt{a^2-b_1^2} $ میرسیم.
خوب، مساحت مثلث برابر با $ \frac{1}{2} bh$ است، پس بجای $h$، در آن $\sqrt{a^2-b_1^2}$ را قرار میدهیم:
$$S= \frac{1}{2}b \sqrt{a^2-b_1^2}$$
حالا باید بجای $b_1$، $\frac{a^2+b^2-c^2}{2b}$ را قرار دهیم:
$$S= \frac{1}{2}b \sqrt{a^2- \big( \frac{a^2+b^2-c^2}{2b} \big)^2}$$
و با سادهسازی و انجام چند عمل جبری ساده بر روی این عبارت، به $\sqrt{( \frac{a+b+c}{2} )(\frac{a+b+c}{2}-a)(\frac{a+b+c}{2}-b)(\frac{a+b+c}{2}-c)}$ میرسیم. در نهایت بدیهی است که اگر بجای $\frac{a+b+c}{2}$، $p$ را قرار دهیم، به فرمول هرون میرسیم.
اثبات بهپایان رسید. امیدوارم لذتبردهباشید.