به نام خدا
همانطور که میدانید، یکی از قضایای مهم در ریاضیات، قضیۀ فیثاغورس است. این قضیه بیان میکند که در هر مثلث قائمالزاویه، مربع اندازۀ ضلع وتر، برابر است با مجموع مربعات اندازۀ دو ضلع دیگر. اثباتهای زیادی برای این قضیه وجود دارد که در این مطلب میتوانید یکی از کوتاهترین و زیباترین این اثباتها را ببینید.
ابتدا مثلث قائمالزاویۀ زیر را در نظر بگیرید:
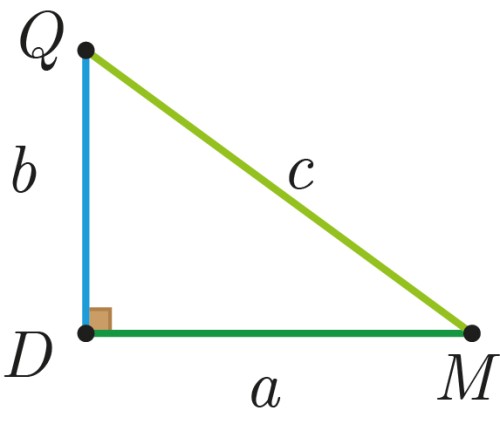
در واقع باید ثابت کنیم که $a^2+b^2=c^2$.
مربعی رسم میکنیم و بعد نقاط $MNPQ$ را به یکدیگر متصل میکنیم تا یک چهار ضلعی درون مربع تشکیل شود:
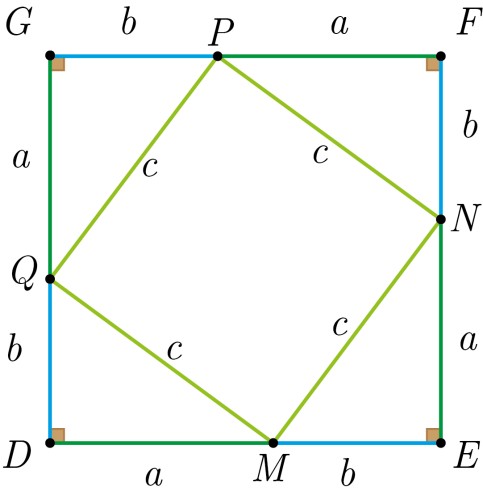
چهار مثلث قائمالزاویۀ تشکیل شده در مربع $DEFG$، باهم به حالت ضزض (دو ضلع و یک زاویۀ بین) همنهشتاند؛ پس اضلاع چهار ضلعی $MNPQ$، باهم برابرند و همچنین میتوان بهراحتی اثبات کرد که $MNPQ$، یک مربع نیز است؛ برای اینکار باید ثابت کنیم که تمام زاویههای آن، $90^{\circ}$ هستند:
$$P\widehat{N}F+F\widehat{P}N+\widehat{F}={180}^{\circ}$$
$$M\widehat{N}E+P\widehat{N}M+P\widehat{N}F={180}^{\circ}$$
$$
\require{cancel}
\Rightarrow \cancel{P\widehat{N}F}+F\widehat{P}N+\widehat{F}=M\widehat{N}E+P\widehat{N}M+\cancel{P\widehat{N}F}
$$
$$
\Rightarrow \cancel{F\widehat{P}N}+90^{\circ}=\cancel{M\widehat{N}E}+P\widehat{N}M
$$
$$\Rightarrow P\widehat{N}M={90}^{\circ}$$
دقت کنید که چون هر چهار مثلث قائمالزاویه با هم همنهشت هستند و در شکلهای همنهشت، زاویههای متناظر باهم برابرند، پس ${F\widehat{P}N}$ با ${M\widehat{N}E}$ برابر است؛ برای همین آن را از دو طرف تساوی خط زدیم. به همین شکل میتوان ثابت کرد که بقیۀ زاویههای $MNPQ$، $90^{\circ}$ هستند.
طول هر ضلع مربع $DEFG$، $a+b$ است؛ بنابراین مساحت این مربع برابر است با:
$$S_{DEFG} = (a+b)^2=a^2+b^2+2ab$$
همچنین مربع $DEFG$، از چهار مثلث قائمالزاویۀ همنهشت و یک مربع تشکیل شدهاست. پس مساحتش را به شکل زیر نیز میتوان نوشت:
$$S_{DEFG}=4\cdot\bigg(\frac{1}{2}ab\bigg)+c^2=2ab+c^2$$
بنابراین:
$$
\require{cancel}
a^2+b^2\cancel{+2ab}=\cancel{2ab}+c^2
$$
$$\Rightarrow a^2+b^2=c^2\ \blacksquare$$