معمولا درک اثبات این قضیه برای دانش آموزان مشکل است چون در همان ابتدای کار باید خطی وارد مساله شود و بیشتر دانش آموزان لزوم این عمل را درک نمی کنند.در ادامه اثباتی مبتنی بر تدریس فعال بیان می شود که به درک اثبات توسظ دانش آموز کمک شایانی می کند.
شروع اثبات: برای درک اثبات ابتدا باید سوال تفهیم شود لذا شکل یک مثلث را کشیده و اضلاع را نامگذاری می کنیم
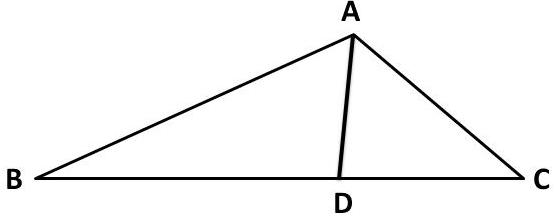
در مرحله بعد حکم را بر اساس شکل پیاده می کنیم یعنی باید ثابت کنیم که
$$ \frac{BD}{DC} = \frac{AB}{AC} $$
از دانش آموزان می خواهیم به حکم توجه کنند که در آن نسبت اضلاع را داریم و از آنان بخواهیم که قضایایی رو که در آنها نسبت اضلاعرا داریم را بیان کنند. معمولا جواب دانش آموزان قضیه تالس و تشابه دو مثلث است(اگر چنین نبود معلم می تواند اسم قضیه را گفته و از دانش آموزان بخواهدکه صورت قضیه را بیان کنند) با توجه به اینکه نه اندازه زاویه و نه هیچ ضلعی را نداریم دانش آموزان را به این مسیر هدایت می کنیم که جواب احتمالا استفاده از قضیه تالس است.
با یاد آوری صورت قضیه تالس(
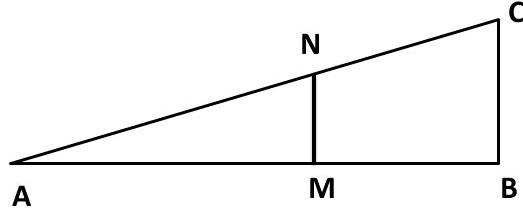
$$\frac{AM}{MB} = \frac{AN}{NC} $$
) و مقایسه حکم با آن به راحتی اکثر دانش آموزان خواهند گفت که باید خطی موازی $AD$ را از راس $C$ را باید داشته باشیم.
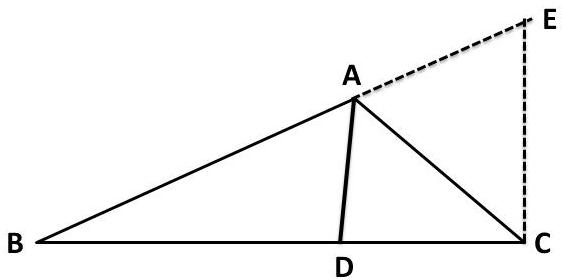
$$\frac{BD}{DC} = \frac{BA}{AE} $$
پس از رسم خط و نوشتن رابطه تالس از دانش آموزان می خواهیم تا آن را با حکم مقایسه کنند و تفاوت این دو را بیان کنند. دانش آموزان خواهند گفت که فقط کافیه به جای $ AE$ داشته باشیم
$AC $.
لذا دانش آموز درک می کند که در گام بعدی باید برابری $ AE $و$ AC $ را ثابت کنیم.
در گام بعد میتوانیم قضیه مثلث متساوی الساقین را یاد آوری کنیم و به دانش آموزان هم یاد آوری کنیم که
$ AD $ خطی عادی نیست بلکه نیمساز است( یا اینکه هنوز از فرض استفاده نشده)
مراحل بعدی اثبات روتین است.