با سلام خوش آمدید
لطفا راهنمای سایت و راهنمای تایپ را مطالعه کنید .
به طور کلی نامعادله های دو متغیره به صورت زیر هستند :
$$f(x,y) > 0\\f(x,y)\geq 0\\f(x,y) < 0\\f(x,y)\leq0$$
چگونه این نامعادله ها را حل کنیم ؟
میدانیم مجموعه جواب های این نامعادلات زیر مجموعه ایی از $\mathbb{R}^2$ است .
برای حل کردن هریک از نامعادله های دو متغییره بالا ابتدا نمودار $f(x,y)=0$ رسم میکنیم
سپس ملاحظه میکنیم که این نمودار این صفحه رو به چند ناحیه تقسیم میکند .
سپس برای بدست اوردن مجموعه جواب نامعادله کافیه که مختصات یک نقطه از هر ناحیه را در نامعادله قرار دهیم چنانچه اون نامعادله به یک نابرابری همیشه درست تبدیل شد .
آنگاه ناحیه ایی که شامل آن نقطه است مجموعه جواب نامعادله خواهد بود .
**مثال **
$$3x+2y > 50$$
$$3x+2y=50\\y=\dfrac{-3}{2}x+25$$
همانطور که میدونید این نمودار یک خط راست است . با رسم آن خواهیم داشت :
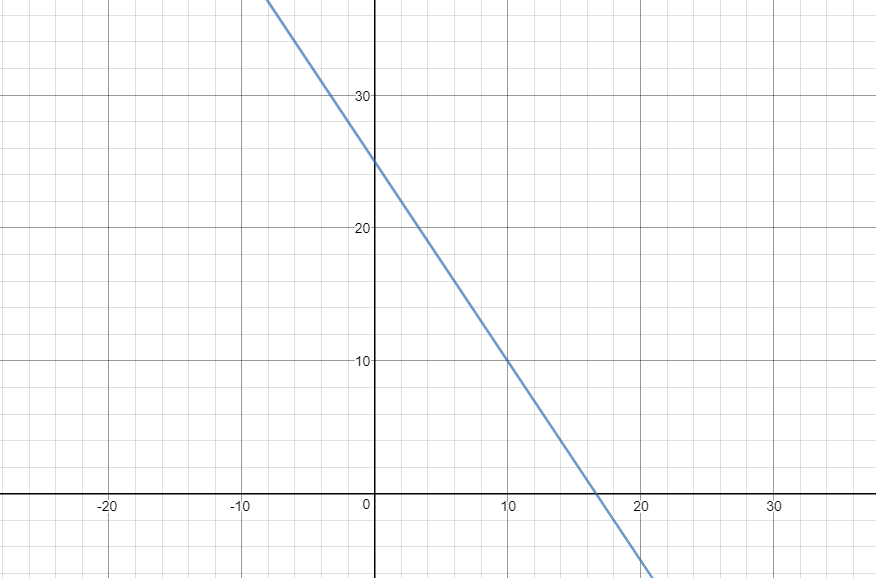
از شکل واضح است صفحه به سه ناحیه تقسیم شده :
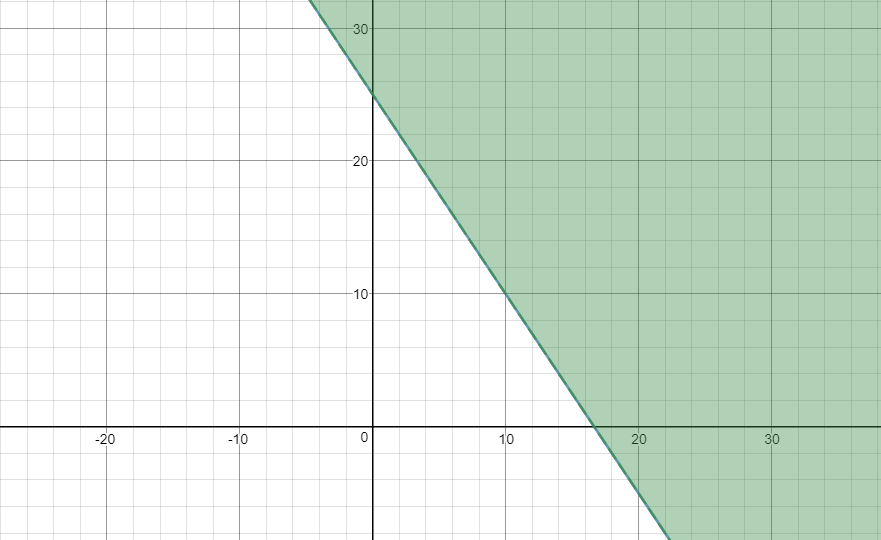
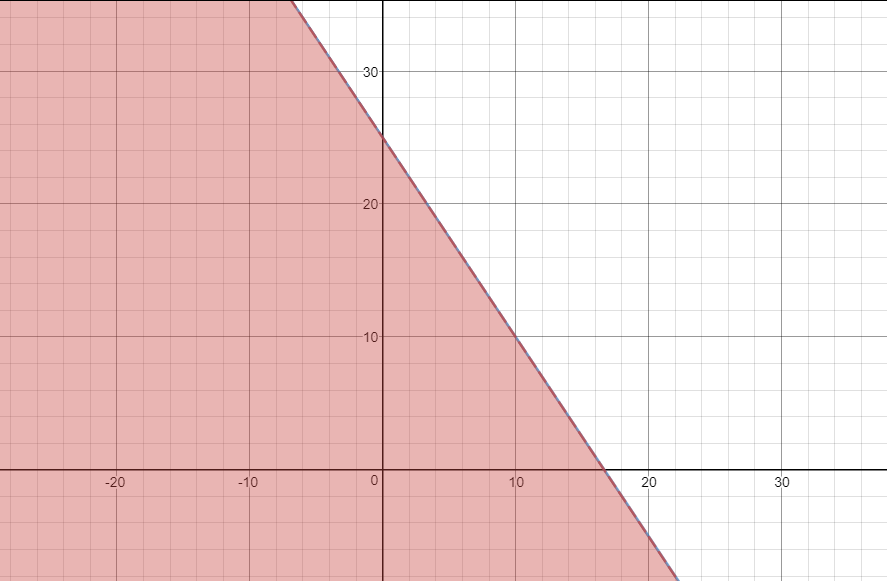
حال از هر ناحیه یک نقطه دلخواه انتخاب میکنیم :
$$A(10,10) \rightarrow 3(10)+2(10) \not\gt50 \tag{1}$$
$$B(20,10) \rightarrow 3(20)+2(10) \gt50 \tag{2}$$
$$C(0,10) \rightarrow 3(0)+2(10) \not\gt50 \tag{3}$$
در نتیجه تنها ناحیه ایی که جواب نامعادله است ناحیه بالای خط $(2)$ است .