روشهای زیادی برای تجسم و رسم و مطالعهٔ بصریِ نمودار یک تابع سهمتغیره هست. در این پاسخ به چند تا از این روشها اشاره میکنیم که با برنامهنویسی مستقیم با یک زبان برنامهنویسی مانند Python یا یک نرمافزار ریاضی پیشرفته میتوانید آنها را پیاده کنید. در این پست من از نرمافزار Mathematica استفاده میکنم ولی تمامی ایدهها را میتوانید در محیطهای دیگر پیاده کنید. تابعتان را در نظر میگیریم.
$$f(x,y,z)=\frac{1}{2}(x+y+z)(2x+3y+5z)$$
نمودار این تابع بر روی مکعب زیر را رسم میکنیم.
$$-1\leq x\leq 1,\;-1\leq y\leq 1,\;-1\leq z\leq 1$$
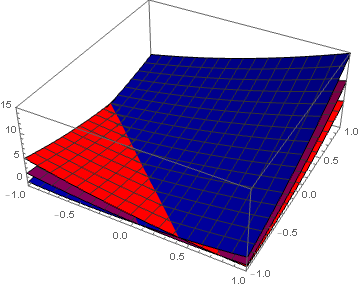
نخستین روش این است که دو متغیر را آزاد بگذارید تا در بازهشان تغییر کنند ولی برای متغیر سومی (انتخاب ترتیب با خودتان است و الزامی ندارد که متغیر سوم حتما $z$ باشد) را برای تعداد متناهی انتخاب در بازهاش مقدار دهید. پس یک چند رویه شکل در یک فضای سهبعدی خواهید گرفت که دو محورش مربوط به دو متغیر آزاد و محور سوم مربوط به $f$ است و متغیر سوم با رنگ تعبیر میشود. برای نمونه در زیر ما متغیرهای $x$ و $y$ را آزاد گذاشته ولی برای متغیر سوم تنها ۳ انتخاب برداشتهایم $z\in\lbrace 0,0.5,1\rbrace$. دوباره تأکید میکنیم که توجه کنید محور بلندی (ارتفاع، عمودی) نشاندهندهٔ $z$ها نیست و نشان دهندهٔ $f(x,y,z)$ است که وقتی $z=0$ رویهٔ قرمزرنگ، وقتی $z=0.5$ رویهٔ بنفشرنگ و وقتی $z=1$ است، رویهٔ آبی رنگ را داریم. دستور و شکل خروجی در زیر آمدهاند.
Plot3D[Evaluate@
Table[(x + y + z)*(2*x + 3*y + 5*z)/2, {z, {0, 0.5, 1}}], {x, -1, 1}, {y, -1, 1},
PlotStyle -> {RGBColor[1, 0, 0], RGBColor[0.5, 0, 0.5],
RGBColor[0, 0, 1]}, PlotRange -> {{-1, 1}, {-1, 1}, {-1, 15}}]
دومین ایده استفاده از نمودار چگالی که برخی به نمودار گرما هم آن را میشناسند است. در این نمودار شما نقطههای دامنه را با توجه به مقدار تابع در آنها رنگآمیزی میکندی و سپس یک نوار مقیاس برای خواندن رنگها در کنارش میگذارید. یک سختی در نمودار چگالی سهبعدی این است که نقاط روبروی هم قرار میگیرند و شما فقط آخرین لایهٔ مجموعه که در معرض دید شماست را میبینید و چیزی که پشت یا درون شکل است را نمیبینید. برای همین باید دامنهٔ سهبعدی را با چیزی دوبعدی قطع دهید و این اشتراک را نگاه کنید. با حرکت دادن این رویهٔ اشتراک میتوانید مقدار تابع در مکانهای متفاوت را ببینید. در نرمافزار Mathematica میتوانید رویهٔ یک مکعب یا رویهٔ یک کره را ببینید (گزینههای دیگر هم دارید که میتوانید در صورت تمایل خودتان پیدا و امتحان کنید). در این حالت طراحان نرمافزار برخی قسمتهای رویه را پررنگ و برخی قسمتها را کمرنگ و حالت نیمهشفاف گذاشتهاند که مثلا پشت کره که در روبروی شما نیست را هم تا حدی ببینید، این کار یک سری معایب هم میتواند داشته باشد ولی به هر حال در خیلی موارد کافی و مفید است. ابتدا دستور و شکل حالت مکعبی را میبینیم.
DensityPlot3D[(x + y + z)*(2*x + 3*y + 5*z)/2, {x, -1, 1}, {y, -1,
1}, {z, -1, 1}, PlotLegends -> Automatic]
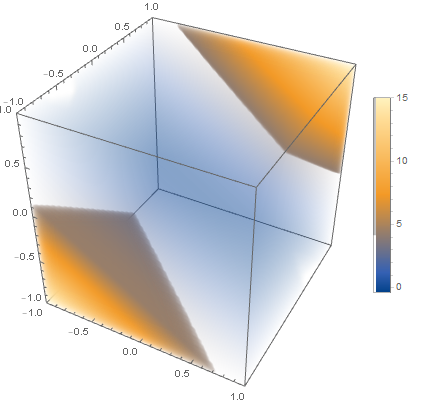
همانطور که میبینی بیشهٔ این تابع در ناحیهٔ خواستهشدهٔ ما که ۱۵ است در دو گوشه اتخاذ میشود و کمینه که صفر است در جایی در میان داخل ناحیه اتخاذ میشود، کمی خواندن این شکل ناساده است بویژه اینکه آبی پررنگ در وسط این شکل شفافشده قرار گرفتهاست ولی اینکه بیشینهها نارنجی سفید و کمرنگشده در دو گوشهٔ $(1,1,1)$ و $(-1,-1,-1)$ اتخاذشدهاست خیلی ساده تشخیص داده میشود و اینکه مقدار تابع هر چه به این دو گوشه نزدیک میشویم افزایش و هر چه به مرکز نزدیکتر میشویم کاهش مییابد. اکنون استفاده از رویهٔ کره.
DensityPlot3D[(x + y + z)*(2*x + 3*y + 5*z)/2, {x, y, z} \[Element]
Ball[{0, 0, 0}, 1], ColorFunction -> Hue, PlotLegends -> Automatic,
AxesLabel -> Automatic]
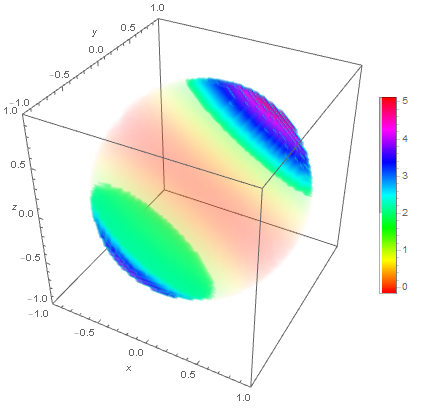
نتیجهٔ مشابهی میگیریم که بیشینه در در قطبی از کره که روی قطر واصل دو گوشهٔ اشاره شده هستند گرفته میشود و در مرکز کره مقدار کمینه گرفته میشود. توجه کنید که شفافکردن قسمتهایی از رویهٔ کره برای اینکه داخل کره هم حس شود باعث سردرگمی در مورد رنگ روی رویهٔ کره در این قسمتها میشود و برای کاربر ممکن است سوال شود که مقدار تابع در قسمت شفاف شده ولی روی رویه چقدر است. اما یک کمک در نمودار مقیاس گذاشتهشدهاست. در کنار برخی نوارها در سمت چپشان رنگ سفید است و در کنار برخی دیگر رنگ خاکستری. رنگ سفید اعلام میکند که نقطههای با این رنگ تحت شفافسازی قرار گرفتهاند و خاکستری اعلام میکند که قسمتهای رویه با این رنگ برایشان شفافسازی صورت نگرفتهاست.
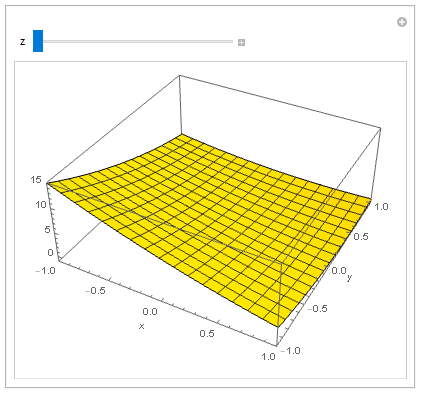
ایدهٔ دیگر استفاده زا animation تصویر متحرک یا برنامَک application-ِ کوچک است که شما یک نوار خواهید داشت مربوط به یک پارامتر که با تکان دادن اهرم این نوار، شکل تغییر میکند پس با جلو عقب بردن این اهرم در واقع کاری که در انیمیشن میشود را برای خودتان انجام میدهید با این تفاوت که سمت حرکت و توقف و همه چیز دست خودتان است تا اینکه یک انیمیشن ذخیره شدهٔ بدون امکان تغییر داشتهباشید. در نرمافزار Mathematica برای ساخت چنین برنامکهایی میتوانید از دستور Manipulate استفاده کنید. در زیر از این ایده به همراه ایدهٔ توضیحدادهشده در ابتدای این پاسخ استفاده میکنیم. یعنی به جای اینکه رویهٔ مقدار تابع را برای چند تعداد متناهی از $z$ در یک شکل با چند رنگ بکشیم، مقدار $z$ را پارامتر برنامکمان میکنیم که با جلو عقب کشیدن اهرم نوار این برنامک نمودار مقدار تابع را برای انتخابهای دلخواه بین مثلا $-1$ تا $1$ از $z$ را میبینیم. دستور و شکل خروجی را در زیر میبینید. البته توجه کنید که در شکل قرار دادهشده در این پست نمیتوانید اهرم را تکان دهید، در صورت تمایل دستور را در نرمافزار Mathematica کپی-پیست کنید و اجرایش کنید یا اینکه دستور را همارزسازی کنید و در نرمافزار موردنظرتان اجرا کنید، برای نمونه نرمافزار Maple نیز چنین قابلیتی دارد.
Manipulate[
Plot3D[(x + y + z)*(2*x + 3*y + 5*z)/2, {x, -1, 1}, {y, -1, 1},
PlotLegends -> Automatic, AxesLabel -> Automatic,
PlotRange -> {{-1, 1}, {-1, 1}, {-1, 15}},
PlotStyle -> Yellow], {z, -1, 1}]
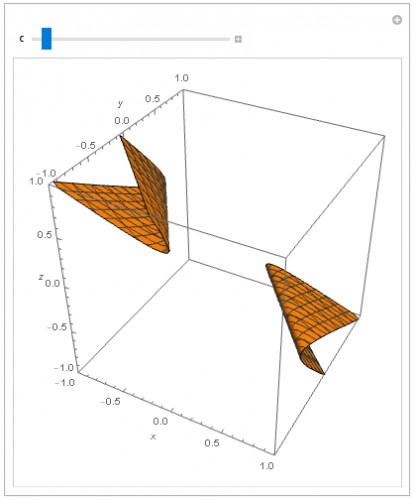
آخرین ایدهای که در اینجا اشاره میکنیم (ولی نه آخرین ایدهٔ ممکن) استفاده از Manipulate ولی این بار به همراه ContourPlot3D است. یعنی برای بازهای از مقادیر، مثلا $[-1,15]$، مجموعهترازهای تابع را رسم میکنیم. به یاد آورید که مجموعهتراز یک زیرمجموعه از دامنه است که تابع بر روی تمام نقاط این مجموعه مقدار یکسانی را میگیرد، در واقع برای هر $c\in\mathbb{R}$، مجموعهترازِ $f$ برای مقدار $c$ برابر است با $f^{-1}(c)$ یک زیرمجموعه از $\mathbb{R}^3$ میشود. دستور و ظاهر خروجی در زیر آوردهشدهاند.
Manipulate[
ContourPlot3D[(x + y + z)*(2*x + 3*y + 5*z)/2 == c, {x, -1,
1}, {y, -1, 1}, {z, -1, 1}, PlotLegends -> Automatic,
AxesLabel -> Automatic,
PlotRange -> {{-1, 1}, {-1, 1}, {-1, 1}}], {c, -1, 15}]