فرض را بر این میگیریم که از «عدد ناوابستگی (استقلال)»-ِ یک گراف زمانی که به «گرهای» یا «یالی» اشاره نمیکنید، به صورت پیشفرض منظورتان «عدد ناوابستگیِ گرهای» بودهاست. یعنی عدد اصلی یک مجموعه از گرههای یک گراف که بین هیچ دوی آنها یالی نتوانید بیابید و مجموعهٔ دیگری از گرههای این گراف که همین ویژگی را داشتهباشد ولی تعداد عضو بیشتری داشته باشد نتوانید یافت. من با نرمافزار GAP، دستکم تا به تاریخ امروز که این پست را مینویسم کار نکردهام ولی نرمافزارهای زیادی هستند که دستورهایی برای کار با گرافها برایشان تعریف شدهاست برای نمونه میتوان نرمافزارهای Maple و Mathematica را نام برد. البته خودتان هم میتوانید با زبانهای برنامهنویسی کدهایی بنویسید که الگوریتمهای مورد نظر را پیاده کند و سپس از کد خودتان استفاده کنید. چون پیشتر در جایی یه نحوهٔ استفاده از نرمافزار Maple برای کار با گرافها اشاره کردهام، در اینجا به نرمافزار Mathematica اشاره میکنم.
نخست تعریف کردن یک گراف در این نرمافزار. برای این کار از دستورِ Graph استفاده میکنیم و در کروشهٔ این دستور باید دو مجموعه را قرار دهید. مجموعهٔ گرهها (رُئوس) را با ابرو (آکولاد) و سپس نوشتن اسمِ گرهها و قرار دادنِ ویرگول در بینشان انجام میدهیم. مجموعهٔ یالها را نیز داخل یک ابرو میگذاریم ولی چگونه یک یال را نمایش دهیم؟ فرض کنید یال وصلکننده از گرهای به نام ۱ به گرهای به نام ۲ را مدنظر داریم. روش یکُم این است که از دستورِ UndirectedEdge[1,2] استفاده کنیم که یک یال بیجهت از بین ۱ و ۲ تعریف میکند. مسلما برای یالهای جهتدار از دستورهای DirectedEdge[u,v] که یک یال جهتدار از $u$ به سمتِ $v$ تعریف میکند و یا دستورِ TwoWayRule[u,v] که یک یال دوطرفه بین این دو گره تعریف میکند استفاده میکنیم. به جایِ DirectedEdge میتوانید از Rule هم استفاده کنید. راه دوم این است که تایپ کنید 1 سپس کلیدِ Esc از صفحه کلید را فشار دهید. سپس تایپ کنید ue که کوتاهشدهٔ undirected edge به معنای یالِ بیجهت است. سپس دوباره کلیدِ Esc از صفحه کلید را بزنید و تایپ کنید 2 نتیجه خودکار به شکل ۱ و ۲ با یک علامت جدید وسطشان میشود که به شکل دوتا نقطهاست که با یک خط به هم وصلشدهاند. این به معنای یالِ بیجهت در Mathematica است. برای یال جهتدار از ۱ به ۲ همین کار را انجام دهید ولی به جای ue از de که کوتاهشدهٔ directed edge به معنای یال جهتدار است استفاده کنید که علامتش شبیه قبلی است ولی نقطهٔ دوم سر پیکان شدهاست. برای یال جهتدار میتوانید بدون استفاده از کلیدِ Esc از صفحهکلید نیز این کار را انجام دهید یعنی کلیدهای منها (خط تیرهٔ معمولی) و سپس علامت بزرگتری که از نظرِ پیکانی رو به راست است را فشار دهید. برای یال دو طرفه علامت کوچکتری، سپس خطتیرهٔ معمولی، سپس علامت بزرگتری را بزنید. Mathematica پس از اینکه کلید ترکیبیِ shift+Enter که برای اجرا کردن خطهای کدتان در این نرمافزار استفاده میکنید را بزنید یک شکل از گرافتان رسم میکند. ما در اینجا دو نمونهٔ ساده انتخاب کردهایم، هر دو گرافتهای با مجموعهٔ $\lbrace 1,2,3,4,5\rbrace$ به عنوان مجموعهٔ گرههایشان هستند. در گرافِ یکُم ۶ یال و در گراف دوم ۱ یال داریم. یالهای گراف نخست گرههای ۱ و ۵ را به گرههای ۲ و ۳ و ۴ وصل میکنند و در گراف دوم یالمان بین گرههای ۱ و ۲ است. اکنون برای داشتن عدد ناوابستگی گرهای کافیست یک مجموعه از گرهها که یالی بینشان نباشد و بیشترین تعداد گره را در بین مجموعههای با خاصیت مشابه دارد پیدا کنیم (توجه کنید که هر مجموعهٔ ماکسیمال ناوابستهای الزاما بیشترین تعداد گرهٔ ممکن را ندارد، ملاک ما اینجا رابطهٔ زیرمجموعه بودن نیست بلکه دقیقا ملاکمان تعداد اعضای مجموعه است). چنین مجموعهای یکتا نیست ولی پیدا کردن یکی هم کار ما را راهمیاندازد. دستورِ ازپیش تعیینشدهای در Mathematica برای این کار وجود دارد؛ FindIndependentVertexSet که در کروشهٔ ورودیاش نام گرافتان را میگذارید. خروجیاش به شکل لیستی از یک لیست است. لیست داخلی مجموعهای است که یافتهاست و ویژگیهای خواستهشدهٔ ما را دارید یعنی بیشترین تعداد ممکن گرهای را دارد که بینشان یالی نیست. اما یک ابرو زیادی دارد برای همین وقتی که میخواهید دستورِ Length که تعداد عضوهای یک لیست را در Mathematica به ما میدهد را رویش پیاده کنیم باید از شرِ ابروی اضافهاش رها شویم. برای این کار میگوئیم عضو نخست لیست بیرونی که لیست درونی میشود را به ما بده، همانطور که در پست دیگری (این پست) اشاره کردیم برای گرفتن عضوِ $i$اُم از یک لیست باید در جلوی نام این لیست یک دوکروشهای باز و بسته کنیم و $i$ را درونش بگذاریم. پس در نهایت کدی که باید بنویسیم برای این دو نمونه به شکل زیر میشوند.
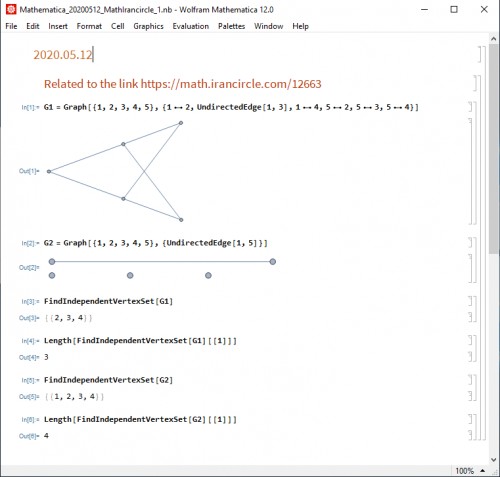
G1= Graph[{1, 2, 3, 4, 5}, {UndirectedEdge[1, 2], UndirectedEdge[1, 3], UndirectedEdge[1,4], UndirectedEdge[5,2], UndirectedEdge[5,3], UndirectedEdge[5,4]}]
G2 = Graph[{1, 2, 3, 4, 5}, {UndirectedEdge[1, 5]}]
FindIndependentVertexSet[G1]
Length[FindIndependentVertexSet[G1][[1]]]
FindIndependentVertexSet[G2]
Length[FindIndependentVertexSet[G2][[1]]]
حاصل اجرا کردن کد بالا در محیط Mathematica (که نوع نماد پس از استفاده از کلیدهای Esc برای یاد بیجهت را هم میتوانید در آن ببینید) را در تصویر زیر آوردهایم.