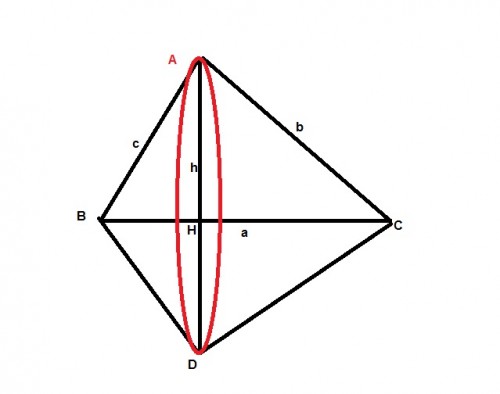
اگر مثلث ABC مثلثی دلخواه باشد ومثلا حول ضلع BC دوران دهیم دو مخروط سمت چپ وراست شکل تشکیل میشود که شعاع قاعده آنها AH وارتفاع آنها یکی BH و دیگریHC میباشد وحجم هردو را بست آورده باهم جمع میکنیم
$ V_{1} = \frac{1}{3} \pi h_{a} ^{2} (BH+HC)= \frac{1}{3} \pi h_{a} ^{2}.a$ که $h_{a} $همان AH میباشد
اگر حجم حاصل از دوران حول ضلع AB را بخواهیم چنین بدست می آید $ V_{2} = \frac{1}{3} \pi h_{c} ^{2}.c$ واگر حجم حاصل از دوران حول AC رابخواهیم $ V_{3} = \frac{1}{3} \pi h_{b} ^{2}.b$اگر نسبت حجم ها را بخواهیم بدست آوریم مثلا$ \frac{V_{1}}{V_{2}} = \frac{\frac{1}{3} \pi h_{a} ^{2}.a}{ \frac{1}{3} \pi h_{c} ^{2}.c} = \frac{ h_{a} ^{2}.a}{ h_{c} ^{2}.c} $
اگر مساحت مخروط ها را بخواهیم بدست آوریم $ S_{1} = \pi h_{a} .c+ \pi h_{a} .b= \pi h_{a} (c+b)$ و
$S_{2} = \pi h_{c} .b+ \pi h_{c} .a= \pi h_{c} (b+a)$ و$S_{3} = \pi h_{b} (c+a)$ که اگر نسبت مساحت ها را بخواهیم مثلا$ \frac{ S_{1} }{ S_{2} } = \frac{ \pi h_{a} (c+b)}{\pi h_{c} (b+a)} = \frac{ h_{a} (c+b)}{h_{c} (b+a)} $
