معادله دایره برابر است با $(x-2a)^2+y^2=a^2$

وقتی این دایره را حول محور y ها دوران دهیم شکلی مثل زیر حاصل می شود که به آن چنبره یا torus می گویند:
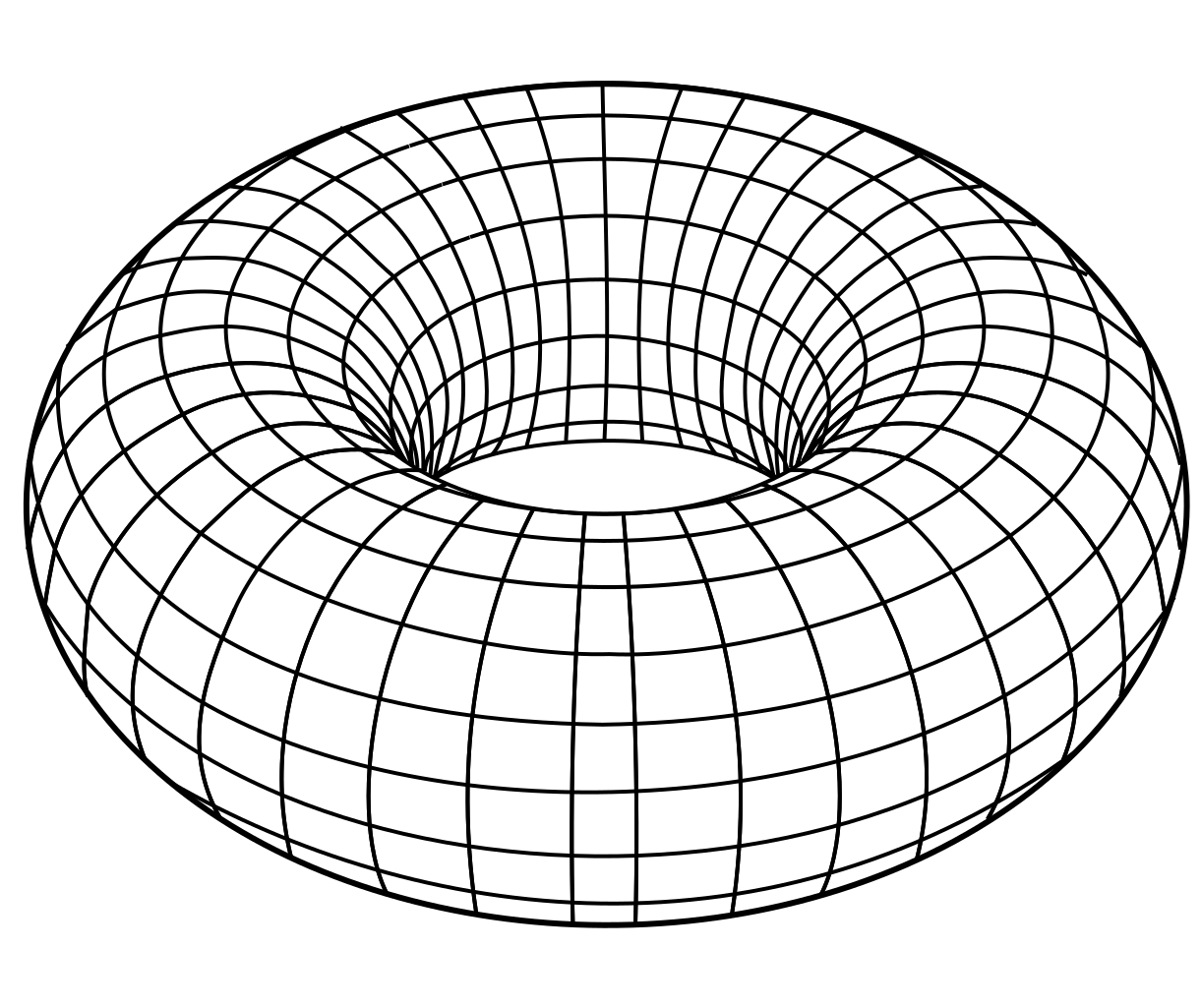
برای به دست آوردن حجم از روش واشر استفاده می کنیم:
$$dV=\pi(R^2-r^2)dy$$
اما $(x-2a)^2=a^2-y^2$ بنابر این $x=2a\pm\sqrt{a^2-y^2}$ پس $R=2a+\sqrt{a^2-y^2}$ و $r=2a-\sqrt{a^2-y^2}$ با محاسبه ای ساده خواهیم داشت:
$$dV=8a\pi\sqrt{a^2-y^2}dy$$
چون $y$ از $-a$ تا $a$ تغییر می کند داریم:
$$V=\int_{-a}^a8a\pi\sqrt{a^2-y^2}dy$$
پس کافی است انتگرال بالا را بیابید که آن هم با یک تغییر متغیر $y=a\sin t$ می توان پیدا کرد:
$$\begin{align}\int_{-a}^a\sqrt{a^2-y^2}dy&=\int_{-\frac\pi2}^{\frac \pi 2}|a\cos t|(a\cos t)dt\\
&=a^2\int_{-\frac \pi2}^{\frac\pi 2}\cos^2t dt\\
&=a^2\int_{-\frac\pi 2}^{\frac \pi 2}\frac{1+\cos 2t}2dt\\
&=a^2(\frac 12t+\frac 14\sin 2t)|_{-\frac\pi 2}^{\frac \pi2}\\
&=a^2(\frac\pi2)\end{align}$$
بنابراین $$V=4a^3\pi^2$$