به روشهای گوناگون میتوانید این حجم را محاسبه کنید. یکی از اینها به کارگیری نکتهٔ زیر که انتگرالگیریِ یگانه دارد است. در کل حجم گردشِ نمودارِ $y=f(x)$ پیرامون محورِ $x$ها با $\int\pi f(x)^2dx$ و حجم گردشِ این نمودار پیرامون محورِ $y$ها با $\int\pi f^{-1}(y)dy$ بدست میآید.
منظور از محور افقی در پرسش، محورِ $x$ها است. پس از فرمولِ نخست میرویم. توجه کنید که شکلِ خواسته شده برابر با دوران نمودارِ $y=e^x$ منهای دوران نمودارِ $y=x^2$ است، پس
\begin{align}
\text{حجم} &= \int_0^1\pi(e^x)^2dx-\int\pi(x^2)^2dx\\
&=\pi\big(\int_0^1(e^{2x}-x^4)dx\big)\\
&=\pi(\frac{1}{2}e^{2x}-\frac{1}{5}x^5)\mid_{x=0}^{x=1}\\
&=\pi(\frac{1}{e^2}-\frac{1}{5}-\frac{1}{2})\\
&\approx 9.41
\end{align}
اگر پرسش نسبت به محور $y$ها را میخواست، آنگاه باید فرمولِ دومی را به کار میبردیم. توجه کنید که در $x=1$ داریم $x^2=1$ و $e^x=e$ پس میتوانیم از خطِ $y=1$ کمک بگیریم و انتگرال را دو قسمت کنیم. بعلاوه توجه کنید که $y=x^2$ به ما $x=\sqrt{y}$ و $y=e^x$ به ما $x=\ln y$ را میدهد.
\begin{align}
\text{حجم} &= \int_0^1\pi(\sqrt{y})^2dy+\int_1^e\pi(\ln y)^2dy\\
&= \pi\big(\int_0^1ydy+\int_1^e(\ln y)^2dy\big)\\
\end{align}
و توجه کنید که با دو بار انتگرال جزء به جزء گرفتن داریم
$$\int(\ln x)^2dx=x(\ln x)^2-2x\ln x+2x$$
پس با محاسبهٔ انتگرالها و جایگذاریِ کرانها داریم
$$\text{حجم}=\pi\big((\frac{1}{2}-0)+(e-2)\big)=e\pi-\frac{3}{2}\pi\approx3.83$$
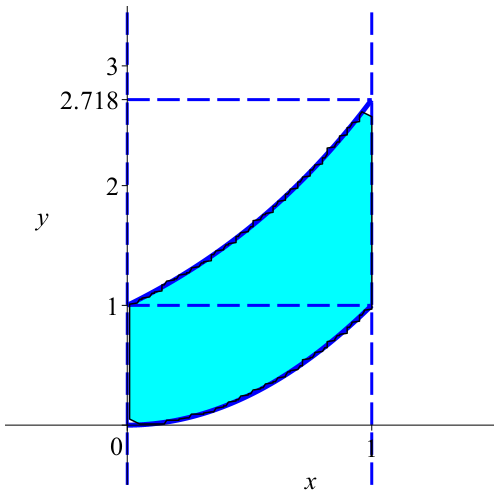
در صورت علاقه، شکل بالا در نرمافزار میپل با دستور زیر کشیدهشدهاست.
p1 := plot( x^2, x = 0..1, thickness = 5, color = blue ):
p2 := plot( exp( x ), x = 0 .. 1, thickness = 5, color = blue ):
p3 := plot( 1, x = 0 .. 1, linestyle = dash, thickness = 3, color = blue ):
p4 := plot( exp( 1 ), x = 0 .. 1, linestyle = dash, thickness = 3, color = blue ):
p5 := plot( [ [ 1, -1 ], [ 1, 4 ] ], style = line, linestyle = dash, thickness = 3 , color = blue ):
p6 := plot( [ [ 0, -1 ], [ 0, 4 ] ], style = line, linestyle = dash, thickness = 3 , color = blue ):
region := piecewise( And( x >= 0, x <= 1, y >= x^2, y <= exp( x ) ), 1, 0 ):
p7 := plots:-implicitplot( region >= 1/2, filled = true, coloring = [ cyan, white ], grid = [ 100, 100 ] ):
plots:-display( p1, p2, p3, p4, p5, p6, p7, view = [ -0.5 .. 1.5, -0.5 .. 3.5 ], labelfont = [ "roman", 20 ], axesfont = [ "roman", 20 ], labels = [ x, y ], tickmarks = [ [ 0, 1], [ 0, 1, 2, exp( 1 ), 3 ] ] );