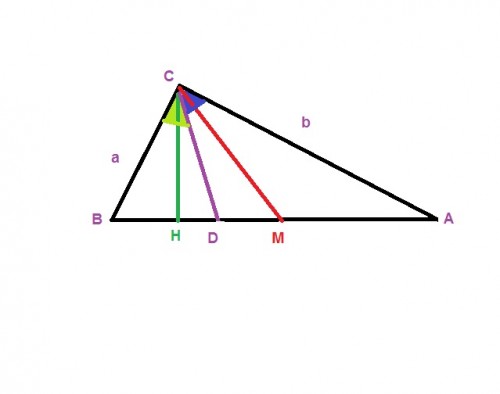
بنام خدا.فرض کنیم در این مثلث ضلع BC کوچکتر از AC باشد اگر CD نیمساز باشد طبق خاصیت نیمساز داریم
$ \frac{a}{b} = \frac{BD}{DA} $ چون طبق فرض صورت از مخرج کوچکتر است داریم
$BD < DA \Rightarrow BD+BD < BD+DA \Rightarrow 2BD < AB \Rightarrow BD < \frac{AB}{2} \Rightarrow BD < BM $
یعنی نقطه D در فاصله کمتر تا نقطه B قرار گرفته است.نقطه H نمی تواند بین M و D قرار گیرد زیرا اگر چنین باشد در این صورت $ \angle B+ \angle BCH=90 و \angle A+ \angle ACH=90 \Rightarrow \angle B+ \angle BCH= \angle A+ \angle ACH$
چون ضلع BC کوچکتر ازAC میباشد ذر نتیجه$ \angle A < \angle B \Rightarrow \angle BCH < \angle ACH$
واین خلاف است زیرا اگر H بین DوM قرار گیرد باید $ \angle BCH > \angle ACH$ چون CD نیمساز است در نتیجه نقطه D بین MوH قرار دارد.
