در مثلث قائم الزاویه میانه وارد بر وتر نصف وتر است.این نکته برای حل مسله کمک میکند. البته میتونه خودش به عنوان سوال مطرح شود!
با فرض اینکه $ \hat{C} > \hat{B} $ داریم:
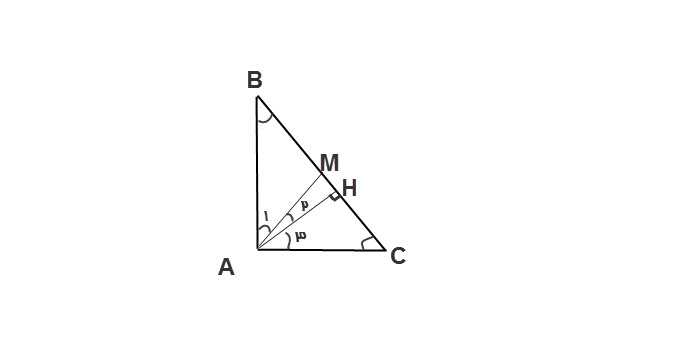
$AM=CM$ (مثلث AMC ،مثلث متساوی الساقین می باشد) در نتیجه
$ \hat{ A_{2} }+ \hat{ A_{3} } =C $$*$
از طرفی $ \hat{ A_{3} }+ \hat{C} =90 $ , $ \hat{B} + \hat{C}=90 $
که نتیجه می دهد $ \hat{A_{3} }= \hat{B} $$**$
بنا به $*$ و $**$ داریم:
$ \hat{ A_{2} }= \hat{C}- \hat{B} $