Question

ثابت کنید مثلثی که میانه نظیر یک ضلع آن نیمساز زاویه مقابل به آن ضلع هم باشد متساوی الساقین است

Answer 1

یک روش ساده استفاده از قانون سینوسها است.

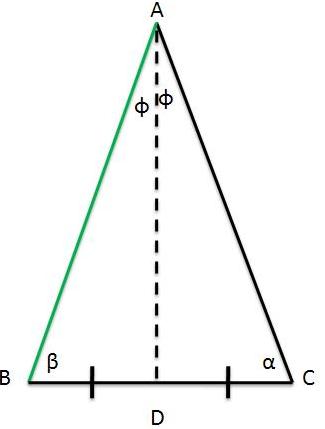
$$ \frac{sin( \phi )}{BD} = \frac{sin( \beta )}{AD} $$ $$ \frac{sin( \phi )}{CD} = \frac{sin( \alpha )}{AD} $$

پس $ sin( \beta )= sin( \alpha )$ و از آنجایی که دو زاویه مکمل نیستند(چرا؟) و هر دو کمتر از 180 و بزرگتر از صفر هستند لذا $ \alpha = \beta $

روش دوم:

از اینکه$ AD $ نمیسازیم است لذا $$ \frac{AB}{AC} = \frac{CD}{BD} =1$$ لذا حکم ثابت میشود

Answer 2

میانه یAMرا به اندازه ی خودش ادامه داده وDMمی نامیم همنهشتی مثلثCMDرابامثلثAMBو سپس با مثلثAMCاثبات می کنیم چون دو مثلث با مثلث دیگر هم نهشتند پس دو مثلثAMBوAMCنیز هم نهشضتند پس مثلث متساوی الساقین است