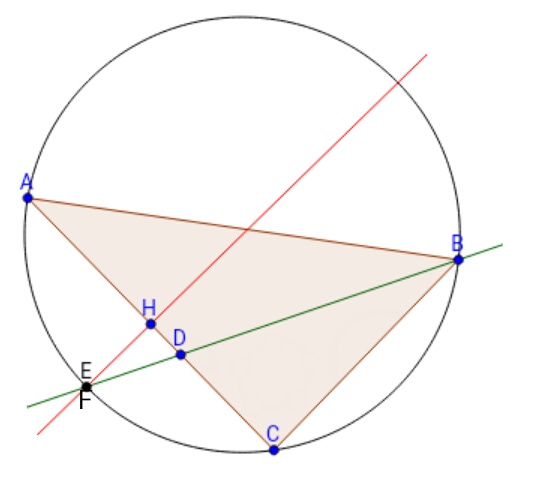
Ш§ЪҜШұ ЩҶЫҢЩ…ШіШ§ШІ $BAC$ ШұШ§ ШұШіЩ… Ъ©ЩҶЫҢЩ…ШҢ Ъ©ЩҮ ШҜШ§ЫҢШұЩҮ ШұШ§ ШҜШұ $E$ ЩӮШ·Ш№ Щ…ЫҢЪ©ЩҶШҜ. ШҜШ§ШұЫҢЩ…:
$$ \hat{BAC}=2 \theta \\ \hat{BAE}=\hat{EAC}=\frac{\hat{BAC}}{2}=\theta \\ \Rightarrow \frown BE=2 \theta=\frown EC \Rightarrow \\ \frown BE+ \frown EC=2 \frown BE=2 \frown EC=\frown BC $$
$(1$ ЩҫШі $E$ ЩҲШіШ· Ъ©Щ…Ш§ЩҶ $BC$ Щ…ЫҢШЁШ§ШҙШҜ.
Ш§ЪҜШұ Ш№Щ…ЩҲШҜ Щ…ЩҶШөЩҒ ШұШ§ ШұШіЩ… Ъ©ЩҶЫҢЩ…ШҢ Ъ©ЩҮ ШҜШ§ЫҢШұЩҮ ШұШ§ ШҜШұ $F$ ЩҲ Ш¶Щ„Ш№ $BC$ ШұШ§ ШҜШұ $H$ ЩӮШ·Ш№ Щ…ЫҢЪ©ЩҶШҜ.
ШҜШұ ЩҶШӘЫҢШ¬ЩҮ ШҜЩҲ Щ…Ш«Щ„Ш« $BHF$ ЩҲ $CHF$ ШЁЩҶШ§ ШЁШұ ШӯШ§Щ„ШӘ (Ш¶ШҢШІШҢШ¶) ЩҮЩ…ЩҶЩҮШҙШӘЩҶШҜШҢ ЩҫШі:
$$ \frac{\frown FC}{2} =\hat{FBC}=\hat{BCF}= \frac{\frown BF}{2} \\ \Rightarrow \frac{\frown BF}{2}+ \frac{ \frown FC}{2}= 2 \frac{ \frown BF}{2}= \frac{ \frown BC}{2} $$
$2($ ЩҫШі $F$ ЩҲШіШ· Ъ©Щ…Ш§ЩҶ $BC$ Ш§ШіШӘ.
Ш§ШІ $1$ ЩҲ $2$ ЩҶШӘЫҢШ¬ЩҮ Щ…ЫҢШҙЩҲШҜ Ъ©ЩҮ:
ЪҶЩҲЩҶ $F$ ЩҲ $E$ ЩҮШұ ШҜЩҲ ШҜШұ ЩҲШіШ· Ъ©Щ…Ш§ЩҶ $BC$ ЩҮШіШӘЩҶШҜ ЩҫШі ШЁШұ ЩҮЩ… Щ…ЩҶШ·ШЁЩӮ Щ…ЫҢШҙЩҲЩҶШҜШҢ ЩҲ ЪҶЩҲЩҶ $F$ ШұЩҲЫҢ Ш№Щ…ЩҲШҜ Щ…ЩҶШөЩҒ ЩҲ $E$ ШұЩҲЫҢ ЩҶЫҢЩ…ШіШ§ШІ ЩҮШіШӘЩҶШҜ ЩҲ $F$ ЩҲ $E$ ЩҮШұ ШҜЩҲ ШұЩҲЫҢ ШҜШ§ЫҢШұЩҮ ЩҮШіШӘЩҶШҜШҢ ЩҫШі ЩҶЫҢЩ…ШіШ§ШІ ЩҲ Ш№Щ…ЩҲШҜ Щ…ЩҶШөЩҒ ЩҮШұ ШҜЩҲ ЩҮЩ…ШҜЫҢЪҜШұ ШұШ§ ШұЩҲЫҢ ШҜШ§ЫҢШұЩҮ Щ…ШӯЫҢШ·ЫҢ Щ…Ш«Щ„Ш« ЩӮШ·Ш№ Щ…ЫҢЪ©ЩҶЩҶШҜ.