ثابت کنید جمع اندازهٔ سه میانه در یک سه گوش دلخواه از محیط سه گوش کمتر ولی از سه چهارم محیط بیشتر است.

Question

ثابت کنید مجموع اندازهٔ هر سه میانهٔ یک مثلث دلخواه همواره از اندازهٔ محیط آن مثلث کوچکتر و از سه‌چهارم محیط بزرگتر است.

Comments

شاید راحت ترین اثباتش با مثلث متساوی الاضلاع باشه
که میانه ها ضلع بزرگتر یک مثلث قائم الزاویه هستند

---

@محمدخوشایند «راحت‌ترین اثبات» یعنی از بین اثبات‌ها برای پرسش که فرضش «سه‌گوش دلخواه» است. پس جملهٔ شما از نظر منطقی و ارزش گزاره‌ای نادرست است. اثبات برای یک سه‌گوش خاص نمی‌تواند یک اثبات برای گزاره در حالت سه‌گوش دلخواه باشد پس اصلا جزو اثبات‌های خواسته‌شده نیست که حالا بخواهد «راحت‌ترین» باشد یا خیر. جملهٔ شما به این شکل درست می‌شود «حکم برای مثلث‌ متساوی‌الأضلاع ساده‌تر بررسی می‌شود» یا «ساده‌ترین حالت برای اثبات، مثلث متساوی‌الأضلاع است».

Answer 1

برای اثبات این گزاره که نوشتید، ابتدا گزاره دیگری را اثبات میکنیم و سپس از طریق آن به اثبات گزاره شما میرسیم. گزاره ای که میخواهیم اثبات کنیم به شرح زیر است:

در هر مثلث دلخواه، اندازه ی میانه ی وارد بر هر ضلع، از نصف مجموع اندازه ی دو ضلع دیگر کوچک تر و از نصف اندازه تفاضل دو ضلع دیگر، بزرگ تر است.

مثلث دلخواه $ABC $ را در نظر میگیریم و میانه وارد بر $BC$ را رسم میکنیم:

حال اگر $AM$ را به اندازه خودش امتداد دهیم داریم:

دو مثلث AMC و DMC با هم به حالت (ض ز ض) هم نهشت هستند. حال نامساوی مثلثی را در مثلث ACD مینویسیم: $$|AD-CD|<AD<AC+CD$$ چون AD دو برابر $m_{a}$ است، پس: $$|AD-CD|<2m_{a}<AC+CD$$ و در نتیجه:

$$\tfrac{|AD-CD|}{2}<m_{a}<\tfrac{AC+CD}{2}$$

و به همین ترتیب برای $m_{b}$ و $m_{c}$ هم داریم:

$$\tfrac{|AB-BC|}{2}<m_{b}<\tfrac{AB+BC}{2} $$ $$\tfrac{|AC-BC|}{2}<m_{c}<\tfrac{AC+BC}{2} $$

حال اگر طرفین نامساوی ها را با هم جمع کنیم، به درستی گزاره شما پی خواهیم برد و اثبات تمام میشود.

Answer 2

بنام خدا

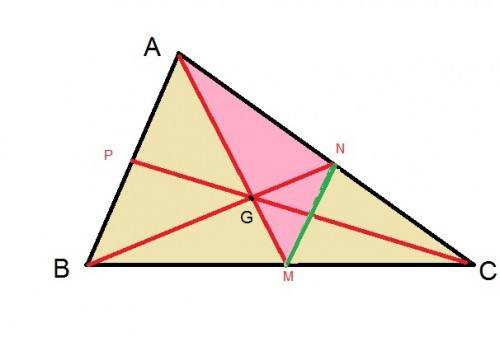
با توجه به شکل بالا چون $M$ و $N$ وسط $BC$ و $AC$ قرار دارند طبق قضیهٔ تالس داریم $MN= \frac{AB}{2} $ حال در مثلث AMN طبق نامساوی مثلث داریم

$$\begin{align} AM & < MN+AN\\ \Longrightarrow AM & < \frac{AB}{2} + \frac{AC}{2} \end{align}$$

به همین ترتیب داریم$BN < \frac{AB}{2} + \frac{BC}{2} $ و $PC < \frac{BC}{2} + \frac{AC}{2} $. حال اگر سه طرف اول سه نامساوی اخیر را جمع کنیم اثبات مجموع سه میانه کوچکتر از مجموع سه ضلع یعنی محیط بدست می‌آید یعنی

$$\begin{align} AM+BN+PC & < \frac{AB}{2} + \frac{AC}{2} + \frac{AB}{2} + \frac{BC}{2} + \frac{BC}{2} + \frac{AC}{2}\\ \Longrightarrow AM+BN+PC & < AB+BC+AC \end{align}$$

برای اثباط قسمت دوم مسأله این قضیه را باید بدانیم که محل تلاقی سه میانه هر مثلث به نسبت $ \frac{2}{3} $ از راس و$ \frac{1}{3} $ از قاعده قطع می‌کنند. مثلا $AG= \frac{2}{3} AM$ حال اگر در مثلث‌های BGC و AGC و AGB نامساوی مثلث‌ها را بنویسیم:

$$\begin{align} BG+GC & > BC \Longrightarrow & \frac{2}{3} BN+ \frac{2}{3} PC & > BC\\ AG+GC & > AC \Longrightarrow & \frac{2}{3} AM+ \frac{2}{3} PC & > AC\\ AG+GB & > AB \Longrightarrow & \frac{2}{3} AM+ \frac{2}{3} BN & > AB \end{align}$$

حال از جمع این سه نامساوی داریم:

$$\begin{align} \frac{4}{3} AM+ \frac{4}{3} BN+ \frac{4}{3} PC & > BC+AC+BC\\ \Longrightarrow AM+BN+PC & > \frac{3}{4} (AB+BC+AC) \end{align}$$

واثبات کامل می‌شود.

Comments

از شما ممنونم