Щ…Ш·Ш§ШЁЩӮ ШҙЪ©Щ„ ШІЫҢШұ Ш§ЪҜШұ Щ…Щ…Ш§Ші ШЁШұ ЩҶЫҢЩ…ШіШ§ШІ Ш№Щ…ЩҲШҜ ШЁШ§ШҙШҜ ЩҫШі ШЁШ§ЫҢШҜ ШІЩҲШ§ЫҢШ§ЫҢ Щ…ШӘЩ…Щ… ЩҶЫҢШІ ШЁШ§ ЩҮЩ… ШЁШұШ§ШЁШұ ШЁШ§ШҙЩҶШҜ.
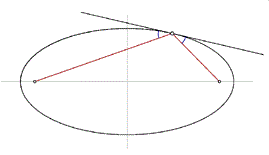
ШӯШ§Щ„ ШЁШ§ ШЁШұЩҮШ§ЩҶ Ш®Щ„ЩҒ Ш«Ш§ШЁШӘ Щ…ЫҢ Ъ©ЩҶЫҢЩ… Ъ©ЩҮ Щ…Щ…Ш§Ші ШЁШұ ЩҶЫҢЩ…ШіШ§ШІ Ш№Щ…ЩҲШҜ Ш§ШіШӘ. ШЁЩҮ ШҙЪ©Щ„ ШІЫҢШұ ШҜЩӮШӘ Ъ©ЩҶЫҢШҜ:
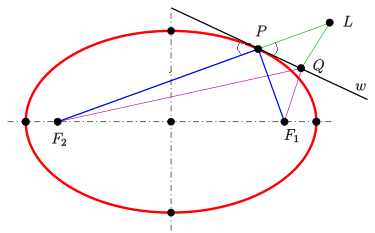
Ш§ЪҜШұ Ш®Ш· w ШҜШұ ЩҶЩӮШ·ЩҮ P Щ…Щ…Ш§Ші ЩҶШЁШ§ШҙШҜШҢ ЩҫШі ШЁШ§ЫҢШҜ ШЁЫҢШ¶ЫҢ ШұШ§ ШҜШұ ЩҶЩӮШ·ЩҮ ШҜЫҢЪҜШұЫҢ Щ…Ш§ЩҶЩҶШҜ Q ЩӮШ·Ш№ Ъ©ЩҶШҜ ЫҢШ№ЩҶЫҢ
В«Ш№ШЁШ§ШұШӘ1В» $QF_{1}+Q F_{2} =PF_{1}+P F_{2} $
ЩҫШ§ШұЩҮ Ш®Ш· PF2 ШұШ§ ШӘШ§ ЩҶЩӮШ·ЩҮ L Ш§Щ…ШӘШҜШ§ШҜ Щ…ЫҢ ШҜЩҮЫҢЩ… ШЁЩҮ ЩҶШӯЩҲЫҢ Ъ©ЩҮ PL=PF1 ШҙЩҲШҜ. ШІШ§ЩҲЫҢЩҮ LPQ=QPF1 Ш®ЩҲШ§ЩҮШҜ ШҙШҜ ШІЫҢШұШ§ ШІШ§ЩҲЫҢЩҮ Щ…ШӘЩӮШ§ШЁЩ„ ШЁЩҮ ШұШ§Ші LPQ ШЁШұШ§ШЁШұ ШІШ§ЩҲЫҢЩҮ QPF1 Ш§ШіШӘ.
ШҜШұ ЩҶШӘЫҢШ¬ЩҮ ШҜЩҲ Щ…Ш«Щ„Ш« PQL ЩҲ PQF1 ЩҮЩ…ЩҶЩҮШҙШӘ ЩҮШіШӘЩҶШҜ. ЩҫШі QL=QF1
ШЁЩҶШ§ШЁШұ ЩӮШ¶ЫҢЩҮ ЩҶШ§Щ…ШіШ§ЩҲЫҢ Щ…Ш«Щ„Ш«ЫҢ
$QL+Q F_{2} >LP+P F_{2} $
ШЁЩҮ Ш¬Ш§ЫҢ PL ЩҲ QL ЩҫШ§ШұЩҮ Ш®Ш· ЩҮШ§ЫҢ ШЁШұШ§ШЁШұШҙШ§ЩҶ ШұШ§ Ш¬Ш§ЫҢЪҜШІЫҢЩҶ Щ…ЫҢ Ъ©ЩҶЫҢЩ….
В«Ш№ШЁШ§ШұШӘ 2В» $QF_{1}+Q F_{2} >PF_{1}+P F_{2} $
ЪҶЩҲЩҶ В«Ш№ШЁШ§ШұШӘ 1В» ЩҲ В«Ш№ШЁШ§ШұШӘ 2В» ШЁШ§ ЩҮЩ… ШӘЩҶШ§ЩӮШ¶ ШҜШ§ШұЩҶШҜ ЩҫШі ЩҒШұШ¶ Щ…Ш§ ШәЩ„Ш· Ш§ШіШӘ ЩҲ Ш®Ш· w ШҜШұ ЩҶЩӮШ·ЩҮ P Щ…Щ…Ш§Ші Ш§ШіШӘ.