این گزاره که هر خمی در هر نقطهاش تنها یک خط مماس دارد نادرست است. گزارهٔ درست «هر خم همواری در هر نقطهاش تنها یک خط مماس دارد» است. «هموار» یعنی چه؟ یعنی بدون نقطهٔ تکینگی. به هر حال بحث این پست نیاز به توضیح بیشتر پیرامون هر خم دلخواه و تعریف تکینگی و خم و غیره ندارد چون در مورد بیضیها است. صرفا برای اینکه ابهامی که ممکن است کاربران بیشتری هم داشتهباشند، یک نمونه خم که در نقطهای دارای بیش از یک خط مماس است میآوریم. خم زیر یک خم خیلی ساده و نامی (مشهور) برای چنین ویژگیای است. به آن خمِ آلفا نیز میگویند به خاطر اینکه شکلش شبیه به حرف یونانیِ آلفا $\alpha$ است. شکل آن در زیر آورده شدهاست که با نرمافزار Maple کشیده شدهاست.
plots:-implicitplot(y^2-x^2-x^3=0,x=-5..5,y=-5..5,'color'='blue',view=[-5..5,-5..5]);
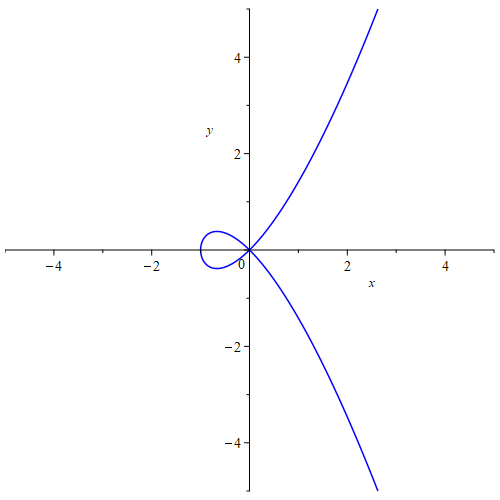
برابریِ تعریفکنندهٔ این خم $y^2=x^2+x^3$ است. برای شیب خط مماس در یک نقطه به محاسبهٔ زیر نگاه کنید.
\begin{align}
y^2=x^2+x^3 &\Longrightarrow 2yy'_x=2x+3x^2\\
&\Longrightarrow y'_x=\frac{2x+3x^2}{2y}
\end{align}
توجه کنید که شیب یعنی $y'_x$ به شکل یک تابع دومتغیره داده شدهاست یعنی ورودیِ آن $(x,y)$ است نه فقط $x$. برای هر نقطهٔ $(x_0,y_0)$ که در برابریِ $y^2=x^2+x^3$ صدق کنند (یعنی بر روی خم هستند) شما یک مقدارِ یکتا از $\mathbb{R}\cup\lbrace\pm\infty\rbrace$ برای خروجیِ $y'_x$ خواهید داشت به جز برای $(0,0)$. در اینجا به $\frac{0}{0}$ برمیخورید که مبهم است و نیاز به رفع ابهام دارد.
\begin{align}
\lim_{(x,y)\to (0,0)}y'_x &= \lim_{(x,y)\to (0,0)}\frac{2x+3x^2}{2y}\\
&= \lim_{x\to 0}\frac{2x+3x^2}{2(\pm\sqrt{x^2+x^3})}\\
& \sim \lim_{x\to 0}\pm\frac{2x}{2|x|}\\
& =\pm 1
\end{align}
چرا مثبتمنها برای نقطههای دیگر رخ نمیدهد؟ پاسخ روشن است، چون برای نقطههای دیگرِ روی خم، نقطه فقط به بخش بالاییِ خم یا به بخش پائینیِ خم تعلق دارد که در بالا $y$ فقط مقدار مثبت پذیرفته است و در پائین تنها مقدار منفی برای $y$ پذیرفته است. از روی شکل نیز میبینید که دقیقا دو خط مماس بر این خم در نقطهٔ $(0,0)$ میتوانید بکشید که یکی نیمساز یکچهارمِ یکُم و سوم است و دیگری نیمساز یکچهارمِ دوم و چهارم.
اما برویم سراغ پرسش اصلی. بدون کاستن از کلیت میتوانید فرض کنید بیضیتان مرکزش مبدأ مختصات است و یکی از دو حالت افقی یا عمودی است. چون جابجایی (انتقال) و چرخش (دوران) تغییری روی تعداد خطهای مماس بر نقطههای منحنی ایجاد نمیکند و دقیقا همان جابجایی و چرخش بر روی آنها هم صورت میگیرد. پس فرض کنید برابریای که بیضیتان را تعریف میکند $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ است. محاسبههای یکسانی با بالا را در اینجا نیز انجام میدهیم.
\begin{align}
\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 &\Longrightarrow \frac{2}{a^2}x+\frac{2}{b^2}yy'_x=0\\
&\Longrightarrow y'_x=-\frac{b^2}{a^2}\frac{x}{y}
\end{align}
توجه کنید که برای هر نقطهٔ $(x_0,y_0)$ به جز $(0,0)$ یک مقدار یکتا از $\mathbb{R}\cup\lbrace\pm\infty\rbrace$ به شما میدهد و خوشبختانه این نقطهٔ $(0,0)$ عضو بیضی نیست چون در برابریمان صدق نمیکند. پس چون مقدار شیب خط مماس در هر نقطه یک عدد یکتا میشود، یک خط مماس هم بیشتر نداریم.