ЩҶЩҲЫҢШіЩҶШҜЩҮ ЩҲШ§ЪҳЩҮЩ” В«Щ…ШӘШ¬Ш§ЩҶШіВ» ШұШ§ ШЁШҜ Ш§ЩҶШӘШ®Ш§ШЁ Ъ©ШұШҜЩҮвҖҢШ§ШіШӘ. ЩҲШ§ЪҳЩҮЩ” Щ…ЩҶШ§ШіШЁ В«ЩҮЩ…ЪҜЩҶВ» Ш§ШіШӘ. ЫҢЪ© ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢ ШұШ§ ЩҮЩ…ЪҜЩҶ ЪҜЩҲЫҢЩҶШҜ ЩҮШұ ЪҜШ§ЩҮ ШҜШұШ¬ЩҮЩ” ШӘЪ© ШӘЪ© Ш¬Щ…Щ„ЩҮвҖҢЩҮШ§ЫҢ ШўЩҶ ШЁШ§ ЩҮЩ… ШЁШұШ§ШЁШұ ШЁШ§ШҙЩҶШҜ. ШЁШұШ§ЫҢ ЩҶЩ…ЩҲЩҶЩҮ $x^5+3x^2y^3$ ЫҢЪ© ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢ ЩҮЩ…ЪҜЩҶ Ш§ШІ ШҜШұШ¬ЩҮЩ” Ыө Ш§ШіШӘ ЩҲЩ„ЫҢ ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢЩҗ $x^2+2x+1$ ЩҮЩ…ЪҜЩҶ ЩҶЫҢШіШӘ. Ш§ЩҶЪҜЩ„ЫҢШіЫҢЩҗ ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢ ЩҮЩ…ЪҜЩҶ Щ…ЫҢвҖҢШҙЩҲШҜ homogeneous polynomial.
Щ…ЩҶШёЩҲШұ ЩҶЩҲЫҢШіЩҶШҜЩҮ Ш§ШІ ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢ Щ…ШӘЩӮШ§ШұЩҶ ЩҶШіШЁШӘ ШЁЩҮ $x_1=x_2$ Ъ©ЩҮ $x_1$ ЩҲ $x_2$ ШҜЩҲ ШӘШ§ Ш§ШІ Щ…ШӘШәЫҢШұЩҮШ§ЫҢ ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢвҖҢШӘШ§ЩҶ Ш§ШіШӘШҢ ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢвҖҢШ§ЫҢ Ш§ШіШӘ Ъ©ЩҮ Щ…Ш¬Щ…ЩҲШ№ЩҮЩ” ШөЩҒШұЩҮШ§ЫҢШҙ ЫҢЪ© ШҙЪ©Щ„ ШЁШіШ§ШІШҜ Ъ©ЩҮ ЩҶШіШЁШӘ ШЁЩҮ Ш§ШЁШұШұЩҲЫҢЩҮЩ” $x_1=x_2$ Щ…ШӘЩӮШ§ШұЩҶ Ш§ШіШӘ. ЩҲЩӮШӘЫҢ ШҜЩҲ Щ…ШӘШәЫҢШұ ШҜШ§ШұЫҢШҜШҢ Ш§ШЁШұ ШұЩҲЫҢЩҮ ЫҢЪ© Ш®Щ… ЫҢЪ© ШЁШ№ШҜЫҢ Щ…ЫҢвҖҢШҙЩҲШҜ. Ш§ШЁШұ ШұЩҲЫҢЩҮ ЫҢШ№ЩҶЫҢ ШұЩҲЫҢЩҮвҖҢШ§ЫҢ Ъ©ЩҮ ШЁЩҸШ№ШҜ ШўЩҶ ЫҢЪ© ЩҲШ§ШӯШҜ Ш§ШІ ШЁШ№ШҜ Ъ©Щ„ ЩҒШ¶Ш§ Ъ©Щ…ШӘШұ Ш§ШіШӘ. ШҜШұ ШӯШ§Щ„ШӘ ШҜЩҲ ШЁШ№ШҜ Ш§ШЁШұШұЩҲЫҢЩҮЩ” $x_1=x_2$ ШҜЩӮЫҢЩӮШ§ ЫҢШ№ЩҶЫҢ Ш®Ш· ЩҶЫҢЩ…ШіШ§ШІ ШұШЁШ№ ЫҢЪ©ЩҸЩ… ЩҲ ШіЩҲЩ…. ШҜШұ ШіЩҮ ШЁШ№ШҜ ЫҢШ№ЩҶЫҢ ШөЩҒШӯЩҮвҖҢШ§ЫҢ Ъ©ЩҮ ЩҶЩӮШ·ЩҮвҖҢЩҮШ§ЫҢШҙ ЫҢЪ© Щ…Ш®ШӘШөвҖҢШҙШ§ЩҶ ШҜЩ„Ш®ЩҲШ§ЩҮ Ш§ЩҶШӘШ®Ш§ШЁ Щ…ЫҢвҖҢШҙЩҲШҜ ЩҲЩ„ЫҢ ШҜЩҲ Щ…Ш®ШӘШө ШҜЫҢЪҜШұШҙ ШЁШ§ ЩҮЩ… ШЁШұШ§ШЁШұ ЩҮШіШӘЩҶШҜ. ЩҲ ШЁШұШ§ЫҢ ШЁШ№ШҜ ШҜЩ„Ш®ЩҲШ§ЩҮ ЩҶЫҢШІ ШЁЩҮ ШұЩҲШҙ Щ…ШҙШ§ШЁЩҮ Ш§ШЁШұШұЩҲЫҢЩҮЩ” $x_1=x_2$ ШӘШ№ШұЫҢЩҒ Щ…ЫҢвҖҢШҙЩҲШҜ.
ШЁШұШ§ЫҢ ЫҢЪ© ЩҶЩ…ЩҲЩҶЩҮЩ” ШўШҙЩҶШ§ ШӘШ§ШЁШ№ $y=\frac{1}{x}$ ШұШ§ ШЁЩҮ ЫҢШ§ШҜШўЩҲШұЫҢШҜ. ЩҶЩ…ЩҲШҜШ§Шұ Ш§ЫҢЩҶ ШӘШ§ШЁШ№ ЩҶШіШЁШӘ ШЁЩҮ ЩҶЫҢЩ…ШіШ§ШІ ЫҢЪ©вҖҢЪҶЩҮШ§ШұЩ… ЫҢЪ©Щ… ЩҲ ШіЩҲЩ… Щ…ШӘЩӮШ§ШұЩҶ ЩҶШЁЩҲШҜШҹ Ш§Ъ©ЩҶЩҲЩҶ ШӘЩҲШ¬ЩҮ Ъ©ЩҶЫҢШҜ Ъ©ЩҮ ЩҶЩ…ЩҲШҜШ§ШұЩҗ Ш§ЫҢЩҶ ШӘШ§ШЁШ№ ШЁШ§ ШҙЪ©Щ„ Щ…Ш¬Щ…ЩҲШ№ЩҮвҖҢЩҫШ§ШіШ®вҖҢЩҮШ§ЫҢ ШЁШұШ§ШЁШұЫҢЩҗ $xy-1=0$ ЫҢЪ©ШіШ§ЩҶ Ш§ШіШӘ. ШЁЩҶШ§ШЁШұШ§ЫҢЩҶ ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢЩҗ $xy-1$ ЩҶШіШЁШӘ ШЁЩҮ $x=y$ Щ…ШӘЩӮШ§ШұЩҶ Ш§ШіШӘ.
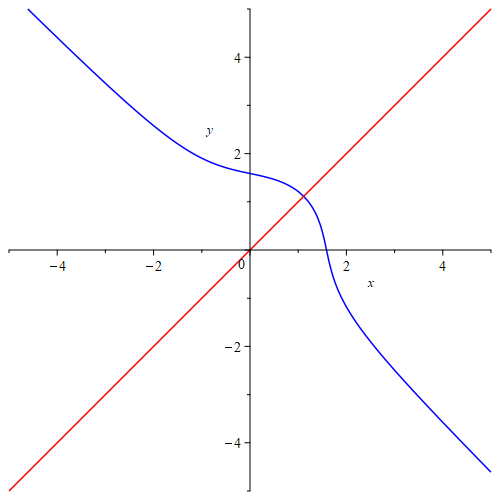
Ш§Ъ©ЩҶЩҲЩҶ ЫҢЪ©ЫҢ Ш§ШІ ЩҶЩ…ЩҲЩҶЩҮвҖҢЩҮШ§ЫҢ Ъ©ШӘШ§ШЁ ШұШ§ ЩҶЪҜШ§ЩҮ Щ…ЫҢвҖҢЪ©ЩҶЫҢЩ…. $x^3+xy+y^3-4$ Щ…Ш¬Щ…ЩҲШ№ЩҮЩ” ШөЩҒШұЩҮШ§ЫҢ Ш§ЫҢЩҶ ШӘШ§ШЁШ№ ШҜЩҲЩ…ШӘШәЫҢШұЩҮ ШұШ§ ШұШіЩ… Щ…ЫҢвҖҢЪ©ЩҶЫҢЩ…. ШҜШұ Ш§ЫҢЩҶШ¬Ш§ Ш§ШІ ЩҶШұЩ…вҖҢШ§ЩҒШІШ§Шұ Maple Ш§ШіШӘЩҒШ§ШҜЩҮ Ъ©ШұШҜЩҮвҖҢШ§ЫҢЩ….
curve1 := plots[implicitplot](x^3 + y^3 + x*y - 4, x = -5 .. 5, y = -5 .. 5, color = 'blue'):
line1 := plot(x, x = -5 .. 5, color = 'red'):
plots[display](curve1, line1);
Ш®Щ…Щҗ ШўШЁЫҢвҖҢШұЩҶЪҜ ШҙЪ©Щ„ Щ…ЩҲШұШҜ ЩҶШёШұ Ш§ШіШӘ ЩҲ Ш®Ш· ЩӮШұЩ…ШІвҖҢШұЩҶЪҜ ЩҶЫҢШіЩ…Ш§ШІ ЫҢЪ©вҖҢЪҶЩҮШ§ШұЩ… ЫҢЪ©Щ… ЩҲ ШіЩҲЩ….
ШЁЩҮ Ш№ЩҶЩҲШ§ЩҶ ЫҢЪ© ШӘЩ…ШұЫҢЩҶ ШіШ§ШҜЩҮ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶЫҢШҜ ШЁШұШ§ЫҢ Ш®ЩҲШҜШӘШ§ЩҶ Ш«Ш§ШЁШӘ Ъ©ЩҶЫҢШҜ Ъ©ЩҮ ШҙЪ©Щ„ ЩҮЩҶШҜШіЫҢ ШөЩҒШұЩҮШ§ЫҢ ЫҢЪ© ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢ $n$ Щ…ШӘШәЫҢШұЩҮ $f$ ШҜШұ ЩҒШ¶Ш§ЫҢ $\mathbb{R}^n$ ЩҶШіШЁШӘ ШЁЩҮ Ш§ШЁШұШұЩҲЫҢЩҮЩ” $x_i=x_j$ Ъ©ЩҮ $i$ ЩҲ $j$ ШҜЩҲ Ш№ШҜШҜ Ш·ШЁЫҢШ№ЫҢ ШЁЫҢЩҶ Ыұ ЩҲ $n$ ЩҲЩ„ЫҢ Щ…Ш®Ш§Щ„ЩҒ ЫҢЪ©ШҜЫҢЪҜШұ ЩҮШіШӘЩҶШҜШҢ ШӘЩӮШ§ШұЩҶ ШҜШ§ШұШҜ Ш§ЪҜШұ ЩҲ ШӘЩҶЩҮШ§ Ш§ЪҜШұ ШҜШұ Ш¶Ш§ШЁШ·ЩҮЩ” $f$ ШЁШ§ ЩҶЩҲШҙШӘЩҶ $x_j$ ШЁЩҮ Ш¬Ш§ЫҢ $x_i$ ЩҲ ЩҶЩҲШҙШӘЩҶ $x_i$ ШЁЩҮ Ш¬Ш§ЫҢ $x_j$ШҢ ШӯШ§ШөЩ„ Ш¶Ш§ШЁШ·ЩҮЩ” ЫҢЪ©ШіШ§ЩҶЫҢ ШҙЩҲШҜ.
ШӘЩҲШ¬ЩҮ Ъ©ЩҶЫҢШҜ Ъ©ЩҮ $x^3+xy+y^3-4$ ШЁШ§ Ш§ЫҢЩҶЪ©ЩҮ ЩҶШіШЁШӘ ШЁЩҮ $x=y$ Щ…ШӘЩӮШ§ШұЩҶ Ш§ШіШӘ ЩҲЩ„ЫҢ ЩҮЩ…ЪҜЩҶ ЩҶЫҢШіШӘ. ШЁШ№Щ„Ш§ЩҲЩҮ ШӘЩҲШ¬ЩҮ Ъ©ЩҶЫҢШҜ Ъ©ЩҮ $x^3+xy+y^3+z$ ЩҶШіШЁШӘ ШЁЩҮ $x=y$ Щ…ШӘЩӮШ§ШұЩҶ Ш§ШіШӘ ЩҲЩ„ЫҢ ЩҶШіШЁШӘ ШЁЩҮ $x=z$ ЫҢШ§ $y=z$ Щ…ШӘЩӮШ§ШұЩҶ ЩҶЫҢШіШӘ. ШІЩ…Ш§ЩҶЫҢЪ©ЩҮ ШӘЩҶЩҮШ§ ШҜЩҲ Щ…ШӘШәЫҢШұ ШҜШ§ШұЫҢШҜ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶЫҢШҜ Ш§ШІ ЪҜЩҒШӘЩҶ В«ЩҶШіШЁШӘ ШЁЩҮ $x=y$В» Ш®ЩҲШҜШҜШ§ШұЫҢ Ъ©ЩҶЫҢШҜ ЪҶЩҲЩҶ ШЁЩҮ Ш·ЩҲШұ ЩҫЫҢШҙвҖҢЩҒШұШ¶ ЩҒЩӮШ· ЩҮЩ…ЫҢЩҶ ШҜЩҲ Щ…ШӘШәЫҢШұ ШұШ§ ШҜШ§ШұЫҢШҜ ЩҲ ЪҜЩҒШӘЩҶ ЩҲ ЩҶЪҜЩҒШӘЩҶ Ш§ЫҢЩҶЪ©ЩҮ Ъ©ШҜШ§Щ… ШҜЩҲ Щ…ШӘШәЫҢШұ ШұШ§ Щ…ШҜЩҶШёШұ ШҜШ§ШұЫҢШҜ ЩҒШұЩӮЫҢ Ш§ЫҢШ¬Ш§ШҜ ЩҶЩ…ЫҢвҖҢЪ©ЩҶШҜ ЩҲ Ш®ЩҲШ§ЩҶЩҶШҜЩҮ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶШҜ ШӯШҜШі ШЁШІЩҶШҜ Щ…ЩҶШёЩҲШұШӘШ§ЩҶ ШӘЩӮШ§ШұЩҶ ЩҶШіШЁШӘ ШЁЩҮ Ъ©ШҜШ§Щ… ШІЩҲШ¬вҖҢЩ…ШӘШәЫҢШұ Ш§ШіШӘ. Ш§Щ…Ш§ ШІЩ…Ш§ЩҶЫҢ Ъ©ЩҮ ШЁЫҢШҙШӘШұ Ш§ШІ ШҜЩҲ Щ…ШӘШәЫҢШұ ШҜШ§ШұЫҢШҜ ШЁШ§ЫҢШҜ Ш§ШҙШ§ШұЩҮ Ъ©ЩҶЫҢШҜ Ъ©ЩҮ ЩҶШіШЁШӘ ШЁЩҮ Ъ©ШҜШ§Щ… ШҜЩҲ Щ…ШӘШәЫҢШұ Щ…ЩҶШёЩҲШұШӘШ§ЩҶ Ш§ШіШӘ Щ…ЪҜШұ Ш§ЫҢЩҶЪ©ЩҮ ШҜЩҲШЁШ§ШұЩҮ ШЁЩҶШ§ ШЁЩҮ ШҜЩ„ЫҢЩ„ЫҢ ЩҒШұШ¶ Ъ©ЩҶЫҢШҜ Ъ©ЩҮ Ш®ЩҲШ§ЩҶЩҶШҜЩҮ Щ…ЩҶШёЩҲШұШӘШ§ЩҶ ШұШ§ ШЁЩҒЩҮЩ…ШҜ. ШҜШұ Ъ©ШӘШ§ШЁ $x^2+y^2+z^2+xy+xz+yz$ ШұШ§ Ш®ЫҢЩ„ЫҢ ШұШ§ШӯШӘ ЪҜЩҒШӘЩҮвҖҢШ§ШіШӘ Щ…ШӘЩӮШ§ШұЩҶ ЩҲ ЩҮЩ…ЪҜЩҶ. ЩҮЩ…ЪҜЩҶ ШЁЩҮ Ш®Ш§Ш·Шұ Ш§ЫҢЩҶЪ©ЩҮ ЩҮШұ Ш¬Щ…Щ„ЩҮ Ш§ШІ ШҜШұШ¬ЩҮЩ” ЫІ Ш§ШіШӘ. Щ…ШӘЩӮШ§ШұЩҶ Щ…ЩҶШёЩҲШұШҙ ЩҶШіШЁШӘ ШЁЩҮ ЩҮШұ ШіЩҮЩ” $x=y$ ЩҲ $x=z$ ЩҲ $y=z$ Ш§ШіШӘ. ЩҲЩ„ЫҢ ЩҮЩ…ЫҢЩҶвҖҢШ·ЩҲШұ Ъ©ЩҮ ШҜЫҢШҜЫҢШҜ Ш§Щ„ШІШ§Щ…ЫҢ ЩҶШҜШ§ШұШҜ Ъ©ЩҮ ЩҶШіШЁШӘ ШЁЩҮ ЩҮШұ ШіЩҮ ШЁШ§ШҙШҜ ШӘШ§ ШЁЩҮ ШўЩҶ Щ…ШӘЩӮШ§ШұЩҶ ЪҜЩҒШӘ. ЩҶЩҲЫҢШіЩҶШҜЩҮ Ш§ШҙШ§ШұЩҮ ЩҶЪ©ШұШҜЩҮвҖҢШ§ШіШӘ ЩҶШіШЁШӘ ШЁЩҮ ЩҮШұ ШіЩҮШҢ ШІЫҢШұШ§ ЩҒШұШ¶ Ъ©ШұШҜЩҮвҖҢШ§ШіШӘ Ш®ЩҲШ§ЩҶЩҶШҜЩҮ Ш®ЩҲШҜШҙ Щ…ШӘЩҲШ¬ЩҮ Щ…ЫҢвҖҢШҙЩҲШҜ Ъ©ЩҮ ЩҶШіШЁШӘ ШЁЩҮ Ъ©ШҜШ§Щ…вҖҢЩҮШ§ ШӘЩӮШ§ШұЩҶ ЩҲШ¬ЩҲШҜ ШҜШ§ШұШҜ.
ЩҲ ШЁШұЩҲЫҢЩ… ШЁЩҮ ШҜЩҶШЁШ§Щ„ ШўШ®ШұЫҢЩҶ Щ…ЩҲШұШҜ. Ш®ЩҲШҜ Ъ©ШӘШ§ШЁ ШҜШұ ЩҮЩҶЪҜШ§Щ… ШӘШ№ШұЫҢЩҒ ШҜЩҲШұЫҢ ШЁЩҲШҜЩҶ ШӘШЈЪ©ЫҢШҜ Ъ©ШұШҜЩҮвҖҢШ§ШіШӘ Ъ©ЩҮ В«Ш§ЪҜШұ $x_1$ ЩҲ $x_2$ ЩҲ ... ЩҲ $x_k$ ЫҢЪ© ШӘШ№ШҜШ§ШҜЫҢ Ш§ШІ Щ…ШӘШәЫҢШұЩҮШ§ ШЁШ§ШҙЩҶШҜ ШўЩҶЪҜШ§ЩҮ ЩҶШіШЁШӘ ШЁЩҮ $x_1,x_2,\dots,x_k$ ШҜЩҲШұЫҢ ЪҜЩҲШҰЫҢЩ… Ш§ЪҜШұ ШЁШ§ ЩҶЩҲШҙШӘЩҶЩҗ $x_{i+1}$ ШЁЩҮ Ш¬Ш§ЫҢ $x_i$ ЩҲ $x_1$ ШЁЩҮ Ш¬Ш§ЫҢ $x_n$ Ш¶Ш§ШЁШ·ЩҮЩ” ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢ ЫҢЪ©ШіШ§ЩҶ ШЁЩ…Ш§ЩҶШҜВ» (Ш§Щ„ШЁШӘЩҮ Щ…ЩҶ ШЁШ§ ЩҶЩ…Ш§ШҜЪҜШ°Ш§ШұЫҢ Ш®ЩҲШҜЩ…Ш§ЩҶ ШЁШ§ШІЩҶЩҲЫҢШіЫҢ Ъ©ШұШҜЩ…). ЫҢШ№ЩҶЫҢ ЪҶЩҮШҹ ЫҢШ№ЩҶЫҢ Ш§ЫҢЩҶЪ©ЩҮ ЩҶЫҢШ§ШІЫҢ ЩҶШҜШ§ШұШҜ ЩҮЩ…ЩҮЩ” Щ…ШӘШәЫҢШұЩҮШ§ ШҜШұЪҜЫҢШұ ШЁШ§ШҙЩҶШҜ. ШЁШұШ§ЫҢ ЩҶЩ…ЩҲЩҶЩҮ ЩҮШұ ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢ Щ…ШӘЩӮШ§ШұЩҶЫҢ ЩҶЫҢШІ ЫҢЪ© ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢ ШҜЩҲШұЫҢ ЩҮЩ… ЩҮШіШӘ. ЪҶШұШ§Шҹ ЪҶЩҲЩҶ Щ…Ш«Щ„Ш§ ЩҒШұШ¶ Ъ©ЩҶЫҢШҜ ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢвҖҢШӘШ§ЩҶ ЩҶШіШЁШӘ ШЁЩҮ $x=y$ Щ…ШӘЩӮШ§ШұЩҶ Ш§ШіШӘ ЩҫШі ШҜЩҲШұЫҢ ЩҶШіШЁШӘ ШЁЩҮ ШҜЩҲШұЩҗ $(x,y)$ ЩҮЩ… ЩҮШіШӘ. ШІЩ…Ш§ЩҶЫҢ Ъ©ЩҮ Щ…ЫҢвҖҢЩҶЩҲЫҢШіЫҢЩ… $(x_1,x_2,\dots,x_k)$ Щ…ЩҶШёЩҲШұЩ…Ш§ЩҶ ШҜЩҲШұЫҢ Ш§ШіШӘ Ъ©ЩҮ $x_1$ ШұШ§ ШЁЩҮ $x_2$ Щ…ЫҢвҖҢШЁШұШҜ ЩҲ ЩҮЩ…ЫҢЩҶШ·ЩҲШұ ШӘШ§ $x_{k-1}$ ШұШ§ ШЁЩҮ $x_k$ ЩҲ $x_k$ ШұШ§ ШЁЩҮ $x_1$. ЩҫШі ЩҮЩ…Ш§ЩҶвҖҢЪҜЩҲЩҶЩҮ Ъ©ЩҮ ШЁШұШ§ЫҢ Щ…ШӘЩӮШ§ШұЩҶ ШЁШ§ЫҢШҜ Ш§ШҙШ§ШұЩҮ Ъ©ЩҶЫҢШҜ Ъ©ЩҮ ЩҶШіШЁШӘ ШЁЩҮ Ъ©ШҜШ§Щ… ШҜЩҲ Щ…ШӘШәЫҢШұШҢ ШЁШұШ§ЫҢ ШҜЩҲШұЫҢ ЩҶЫҢШІ ШЁШ§ЫҢШҜ Ш§ШҙШ§ШұЩҮ Ъ©ЩҶЫҢШҜ ЩҶШіШЁШӘ ШЁЩҮ Ъ©ШҜШ§Щ… ШҜЩҲШұ Щ…ЪҜШұ Ш§ЫҢЩҶЪ©ЩҮ ЩҒШұШ¶ ШҙЩҲШҜ Ъ©ЩҮ Ш®ЩҲШ§ЩҶЩҶШҜЩҮ Щ…ШӘЩҲШ¬ЩҮ ШҜЩҲШұЩҗ Щ…ЩҲШұШҜ ЩҶШёШұ ШҙЩ…Ш§ Щ…ЫҢвҖҢШҙЩҲШҜ. ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢ ШҜЩҲШұЫҢ ШЁЩҮ Ш§ЩҶЪҜЩ„ЫҢШіЫҢ Щ…ЫҢвҖҢШҙЩҲШҜ cyclic polynomial. ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢ Щ…ШӘЩӮШ§ШұЩҶ ЩҶЫҢШІ ШЁЩҮ Ш§ЩҶЪҜЩ„ЫҢШіЫҢ symmetric polynomial Щ…ЫҢвҖҢШҙЩҲШҜ.
Ш§ЫҢЩҶЪ© Ш§ЪҜШұ ШҜШұШі Ш¬ШЁШұ Ыұ ШҜЩҲШұЩҮЩ” Ъ©Ш§ШұШҙЩҶШ§ШіЫҢ ШұЫҢШ§Ш¶ЫҢ ШұШ§ ЪҜШ°ШұШ§ЩҶШҜЩҮ ШЁШ§ШҙЫҢШҜ ШЁШ§ ЪҜШұЩҲЩҮ Ш¬Ш§ЫҢЪҜШҙШӘвҖҢЩҮШ§ ШўШҙЩҶШ§ ШҙШҜЩҮвҖҢШ§ЫҢШҜ. Ш§ЪҜШұ Ш®ЫҢШұ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶЫҢШҜ ШЁЩҮ ЫҢЪ© Щ…ЩҶШЁШ№ Ш¬ШЁШұ ШҜЩҲШұЩҮЩ” Ъ©Ш§ШұШҙЩҶШ§ШіЫҢ Щ…Ш§ЩҶЩҶШҜ Ъ©ШӘШ§ШЁ В«Ш¬ШЁШұВ»ШҢ ЩҶЩҲШҙШӘЩҮЩ” В«Ш№Щ„ЫҢвҖҢШ§Ъ©ШЁШұ Щ…ШӯЩ…ШҜЫҢ ШӯШіЩҶвҖҢШўШЁШ§ШҜЫҢВ»ШҢ Ш§ЩҶШӘШҙШ§ШұШ§ШӘ ШҜШ§ЩҶШҙЪҜШ§ЩҮ Ш§ШөЩҒЩҮШ§ЩҶ ЫҢШ§ Ъ©ШӘШ§ШЁ Abstract Algebra ЩҶЩҲШҙШӘЩҮЩ” Foote ЩҲ Dummit ЩҶЪҜШ§ЩҮ Ъ©ЩҶЫҢШҜШҢ ЫҢШ§ Ш§ЫҢЩҶЪ©ЩҮ Ш§ШІ Ш®ЩҲШ§ЩҶШҜЩҶ Ш§ШҜШ§Щ…ЩҮЩ” Ш§ЫҢЩҶ ЩҫШ§ШіШ® ШөШұЩҒ ЩҶШёШұ Ъ©ЩҶЫҢШҜ ЪҶЩҲЩҶ ШӘШ§ Ш¬Ш§ЫҢЫҢ Ъ©ЩҮ Ъ©ШӘШ§ШЁ Щ…ЩҶШёЩҲШұ ШҜШ§ШҙШӘЩҮвҖҢШ§ШіШӘ ШҜШұ ШЁШ§Щ„Ш§ ШұЩҲШҙЩҶ ШҙШҜЩҮвҖҢШ§ШіШӘ. ЫҢЪ© Щ…Ш¬Щ…ЩҲШ№ЩҮЩ” Щ…ШӘЩҶШ§ЩҮЫҢЩҗ $n$ Ш№Ш¶ЩҲЫҢ ШұШ§ ШҜШұ ЩҶШёШұ ШЁЪҜЫҢШұЫҢШҜ. ЫҢЪ© Ш¬Ш§ЫҢЪҜШҙШӘ ЫҢЪ© ШӘШ§ШЁШ№ ЫҢЪ©вҖҢШЁЩҮвҖҢЫҢЪ© ЩҲ ЩҫЩҲШҙШ§ Ш§ШІ Ш§ЫҢЩҶ Щ…Ш¬Щ…ЩҲШ№ЩҮ ШЁЩҮ Ш®ЩҲШҜШҙ Ш§ШіШӘ. ШҜШұ ЩҲШ§ЩӮШ№ Ш§ШІ Ш§ШіЩ…Шҙ ШұЩҲШҙЩҶ Ш§ШіШӘ Ъ©ЩҮ ЫҢШ№ЩҶЫҢ Ш§Ш№Ш¶Ш§ Ш¬Ш§ЫҢШҙШ§ЩҶ ШұШ§ ШЁЩҮ ЩҮЩ… Щ…ЫҢвҖҢШҜЩҮЩҶШҜ ЩҲ ЫҢЪ© ЪҜШҙШӘ Ш§ЫҢШ¬Ш§ШҜ Щ…ЫҢвҖҢШҙЩҲШҜ. Ш§Щ„ШЁШӘЩҮ Ш§Щ„ШІШ§Щ…ЫҢ ЩҶШҜШ§ШұШҜ Ъ©ЩҮ ЩҮЩ…ЩҮ Ш§ЫҢЩҶ Ъ©Ш§Шұ ШұШ§ ШЁЪ©ЩҶЩҶШҜ. ШЁШұШ§ЫҢ ЩҶЩ…ЩҲЩҶЩҮ Ш§ЪҜШұ Щ…Ш¬Щ…ЩҲШ№ЩҮЩ”вҖҢЩ…Ш§ЩҶ $\lbrace 1,2,3,4,5\rbrace$ ШЁШ§ШҙШҜ ЫҢЪ© Ш¬Ш§ЫҢЪҜШҙШӘ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶШҜ Ш§ЫҢЩҶЪҜЩҲЩҶЩҮ ШЁШ§ШҙШҜ Ъ©ЩҮ Ыұ ШұШ§ ШЁЩҮ ЫІ ЩҲ ЫІ ШұШ§ ШЁЩҮ Ыі ЩҲ ШіЩҫШі Ыі ШұШ§ ШЁЩҮ Ыұ Ш¬Ш§ШЁШ¬Ш§ Ъ©ЩҶЫҢЩ… ЩҲ Ыҙ ЩҲ Ыө ШұШ§ ШіШұ Ш¬Ш§ЫҢШҙШ§ЩҶ ЩҶЪҜЩҮ ШҜШ§ШұЫҢЩ…. Ш§ЫҢЩҶ Ш¬Ш§ЫҢЪҜШҙШӘ ШұШ§ ШЁШ§ ЩҶЩ…Ш§ШҜЩҮШ§ Ш§ЫҢЩҶЪҜЩҲЩҶЩҮ ЩҶЩ…Ш§ЫҢШҙ Щ…ЫҢвҖҢШҜЩҮЫҢЩ….
$$\begin{pmatrix}
1 & 2 & 3 & 4 & 5\\
2 & 3 & 1 & 4 & 5
\end{pmatrix}$$
ЩҲ ЩҶШӯЩҲЩҮЩ” ШӘШ№ШЁЫҢШұШҙ Ш§ЫҢЩҶ Ш§ШіШӘ Ъ©ЩҮ ШіШ·Шұ ЩҶШ®ШіШӘ Ш§Ш№Ш¶Ш§ ШұШ§ ШЁШ§ ЩҮШұ ШӘШұШӘЫҢШЁЫҢ Ъ©ЩҮ ШЁШ®ЩҲШ§ЩҮЫҢШҜ ШҜШ§ШұШҜ ЩҲ ШіШ·Шұ ШҜЩҲЩ… ЩҶШҙШ§ЩҶ Щ…ЫҢвҖҢШҜЩҮШҜ Ъ©ЩҮ Ш№Ш¶ЩҲ ШЁШ§Щ„Ш§ЫҢ ШіШұШҙ ШЁЩҮ ЪҶЩҮ ЪҶЫҢШІЫҢ ЩҶЪҜШ§ШҙШӘЩҮ ШҙШҜЩҮ Ш§ШіШӘ. Ш§ЪҜШұ ШӘЩҲШ¬ЩҮ Ъ©ЩҶЫҢШҜ Ш§ЫҢЩҶ Ш¬Ш§ЫҢЪҜШҙШӘ ЫҢЪ© ШҜЩҲШұ ШЁЫҢЩҶ ШіЩҮ Ш№Ш¶ЩҲ Ыұ ЩҲ ЫІ ЩҲ Ыі Ш§ШіШӘ. ЫҢШ§ ШҜШұ ЩҲШ§ЩӮШ№ Ыі ШҜЩҲШұ Ш§ШіШӘ Ъ©ЩҮ ШҜЩҲШұ ШҜЩҲЩ… ЩҲ ШіЩҲЩ… ШЁШҜЫҢЩҮЫҢ ЩҮШіШӘЩҶШҜ ЩҲ Ш№Ш¶ЩҲЫҢ ШұШ§ ШЁЩҮ Ш®ЩҲШҜШҙ Щ…ЫҢвҖҢШЁШұЩҶШҜ ЩҲ ШӘЩ…Ш§Щ…. ШЁШ§ ЩҶЩ…Ш§ШҜЪҜШ°Ш§ШұЫҢвҖҢШ§ЫҢ Ъ©ЩҮ ЩҫЫҢШҙвҖҢШӘШұ ЩҮЩ… ШҜЫҢШҜЫҢШҜ Ш§ЫҢЩҶ ШіЩҮ ШҜЩҲШұ ШЁЩҮ ШҙЪ©Щ„Щҗ $(1,2,3)$ ЩҲ $(4)$ ЩҲ $(5)$ ЩҶЩ…Ш§ЫҢШҙ ШҜШ§ШҜЩҮ Щ…ЫҢвҖҢШҙЩҲЩҶШҜ. Щ…Ш№Щ…ЩҲЩ„Ш§ ШҜЩҲШұЩҮШ§ЫҢ ШЁШҜЫҢЩҮЫҢ Щ…Ш§ЩҶЩҶШҜ $(4)$ ШұШ§ ЩҶЩ…ЫҢвҖҢЩҶЩҲЫҢШіЩҶШҜ ЪҶЩҲЩҶ ШҜШ§ШҜЩҮЩ” Ш¬ШҜЫҢШҜЫҢ ШЁЩҮ Щ…Ш§ ЩҶЩҲШҙШӘЩҶШҙ ЩҶЩ…ЫҢвҖҢШҜЩҮШҜ. ШЁЩҮ ЩҮШұ ШӯШ§Щ„ШҢ ЫҢЪ© ШҜЩҲШұ Ъ©ЩҮ $k$ Ш№Ш¶ЩҲ ШҜШ§ШұШҜ ШұШ§ Ш§ШІ Щ…ШұШӘШЁЩҮЩ” $k-1$ Щ…ЫҢвҖҢЪҜЩҲЫҢЩҶШҜ. ЫҢЪ© ШҜЩҲШұ Ш§ШІ Щ…ШұШӘШЁЩҮЩ” Ыұ ШұШ§ ЫҢЪ© ШӘШұШ§ЩҶЩҮШҙШӘ ЩҶЫҢШІ Щ…ЫҢвҖҢЪҜЩҲЫҢЩҶШҜ. ШЁШұШ§ЫҢ ЩҶЩ…ЩҲЩҶЩҮ $(x,y)$ ЫҢЪ© ШӘШұШ§ЩҶЩҮШҙШӘ ШЁШұ ШұЩҲЫҢ Щ…Ш¬Щ…ЩҲШ№ЩҮЩ” Щ…ШӘШәЫҢШұЩҮШ§ЫҢ ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢвҖҢШӘШ§ЩҶ Ш§ШіШӘ.
ШӘЩҲШ¬ЩҮ Ъ©ЩҶЫҢШҜ Ъ©ЩҮ ЩҮШұ Ш¬Ш§ЫҢЪҜШҙШӘЫҢ Ш§Щ„ШІШ§Щ…Ш§ ЫҢЪ© ШҜЩҲШұ ЩҶЫҢШіШӘ. Щ…Ш¬Щ…ЩҲШ№ЩҮЩ” Ш¬Ш§ЫҢЪҜШҙШӘвҖҢЩҮШ§ЫҢ ШұЩҲЫҢ $n$ Ш№Ш¶ЩҲ ШұШ§ ШЁШ§ $S_n$ ЩҶЩ…Ш§ЫҢШҙ Щ…ЫҢвҖҢШҜЩҮЩҶШҜ. Ш§ЩҶЪҜЩ„ЫҢШіЫҢ ЩҲШ§ЪҳЩҮЩ” Ш¬Ш§ЫҢЪҜШҙШӘ permutation Ш§ШіШӘ. Ш§Ъ©ЩҶЩҲЩҶ ЪҶЫҢШІЫҢ Ъ©ЩҮ Щ…ЩҶШӘШёШұШҙ ШЁЩҲШҜЫҢЩ…. ЫҢЪ© ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢ ШЁШ§ $n$ Щ…ШӘШәЫҢШұ ШұШ§ ШҜШұ ЩҶШёШұ ШЁЪҜЫҢШұЫҢШҜ. ЫҢЪ© Ш¬Ш§ЫҢЪҜШҙШӘ Ш§ШІ $S_n$ ШұШ§ ЫҢЪ© ЩҶШ§ЩҲШұШҜШ§ ШЁШұШ§ЫҢ Ш§ЫҢЩҶ ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢ Щ…ЫҢвҖҢЪҜЩҲШҰЫҢЩ… ЩҮШұ ЪҜШ§ЩҮ Ш§Ш«Шұ ШҜШ§ШҜЩҶ Ш§ЫҢЩҶ Ш¬Ш§ЫҢЪҜШҙШӘ ШұЩҲЫҢ Щ…ШӘШәЫҢШұЩҮШ§ ШҜШұ Ш§ЫҢЩҶ ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢШҢ Ш¶Ш§ШЁШ·ЩҮЩ” ШўЩҶ ШұШ§ ШӘШәЫҢЫҢШұ ЩҶШҜЩҮШҜ. ЩҫШі ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢвҖҢЩҮШ§ЫҢ Щ…ШӘЩӮШ§ШұЩҶ ШҜШұ ЩҲШ§ЩӮШ№ ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢвҖҢЩҮШ§ЫҢЫҢ ЩҮШіШӘЩҶШҜ Ъ©ЩҮ ШҜШ§ШұШ§ЫҢ ЩҶШ§ЩҲШұШҜШ§ЫҢ ШӘШұШ§ЩҶЩҮШҙ ЩҮШіШӘЩҶШҜШҢ ЩҲ ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢвҖҢЩҮШ§ЫҢ ШҜЩҲШұЫҢШҢ ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢвҖҢЩҮШ§ЫҢЫҢ ЩҮШіШӘЩҶШҜ Ъ©ЩҮ ШҜШ§ШұШ§ЫҢ ЩҶШ§ЩҲШұШҜШ§ШұЫҢ ШҜЩҲШұ ЩҮШіШӘЩҶШҜ. ЪҶЩҲЩҶ ЫҢЪ© ШӘШұШ§ЩҶЩҮШҙ ЫҢЪ© ШҜЩҲШұ ЩҶЫҢШІ Ш§ШіШӘ ЩҫШі ШұЩҲШҙЩҶ Ш§ШіШӘ Ъ©ЩҮ ЫҢЪ© ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢ Щ…ШӘЩӮШ§ШұЩҶШҢ ШҜЩҲШұЫҢ ЩҶЫҢШІ Ш§ШіШӘ. Ш§ЩҶЪҜЩ„ЫҢШіЫҢ ЩҶШ§ЩҲШұШҜШ§ invariant Ш§ШіШӘ. ЩӮШ¶ЫҢЩҮвҖҢЩҮШ§ ЩҲ ЩҶШӘШ§ЫҢШ¬ ШІЫҢШ§ШҜЫҢ ШҜШұ ЩҮЩҶШҜШіЩҮЩ” Ш¬ШЁШұЫҢ ЩҫЫҢШұШ§Щ…ЩҲЩҶ ЩҶШ§ЩҲШұШҜЩҮШ§ЫҢ ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢвҖҢЩҮШ§ ЩҮШіШӘ Ъ©ЩҮ ШҜШұ ШөЩҲШұШӘ Ш№Щ„Ш§ЩӮЩҮ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶЫҢШҜ ЪҜШҙШӘ ЩҲ ЪҜШ°Ш§ШұЫҢ ШҜШұ ШўЩҶЩҮШ§ Ш§ЩҶШ¬Ш§Щ… ШҜЩҮЫҢШҜ.
ШҜШұ ЩҶШұЩ…вҖҢШ§ЩҒШІШ§ШұЩҮШ§ЫҢ ШұЫҢШ§Ш¶ЫҢ ШҜШіШӘЩҲШұЩҮШ§ЫҢ ШўЩ…Ш§ШҜЩҮ ШЁШұШ§ЫҢ ШӘШ№ШұЫҢЩҒ ЩҲ Ш§ШіШӘЩҒШ§ШҜЩҮЩ” Ш¬Ш§ЫҢЪҜШҙШӘвҖҢЩҮШ§ ЩҲШ¬ЩҲШҜ ШҜШ§ШұШҜ. ШЁШұШ§ЫҢ ЩҶЩ…ЩҲЩҶЩҮ ШҜШіШӘЩҲШұ Perm (Ъ©ЩҮ Ш§ШІ Ш§ШЁШӘШҜШ§ЫҢ ЩҲШ§ЪҳЩҮЩ” permutation Щ…ЫҢвҖҢШўЫҢШҜ) ШЁШұШ§ЫҢ ШӘШ№ШұЫҢЩҒ Ш¬Ш§ЫҢЪҜШҙШӘ Ш§ШіШӘЩҒШ§ШҜЩҮ Щ…ЫҢвҖҢШҙЩҲШҜ. ЩҲЩ„ЫҢ ШӘЩҲШ¬ЩҮ Ъ©ЩҶЫҢШҜ Ъ©ЩҮ Ш·ШұШ§ШӯвҖҢЩҮШ§ЫҢ Ш§ЫҢЩҶ ЩҶШұЩ…вҖҢШ§ЩҒШІШ§Шұ ЩҲШұЩҲШҜЫҢЩҗ Ш§ЫҢЩҶ ШҜШіШӘЩҲШұ ШұШ§ ШӘЩҶЩҮШ§ Ш№ШҜШҜЩҮШ§ЫҢ Ш·ШЁЫҢШ№ЫҢ ЪҜШұЩҒШӘЩҮвҖҢШ§ЩҶШҜ ШЁЩҶШ§ШЁШұШ§ЫҢЩҶ Ш§ЪҜШұ Ш§ШІ Ш§ЫҢЩҶ ШҜШіШӘЩҲШұ Щ…ЫҢвҖҢШ®ЩҲШ§ЩҮЫҢШҜ Ш§ШіШӘЩҒШ§ШҜЩҮ Ъ©ЩҶЫҢШҜ ШЁЩҮ Ш¬Ш§ЫҢ $x$ ЩҲ $y$ ЩҲ $z$ ШЁЩҮШӘШұ Ш§ШіШӘ Ш§ШІ $x_1$ ЩҲ $x_2$ ЩҲ $x_3$ Ш§ШіШӘЩҒШ§ШҜЩҮ Ъ©ЩҶЫҢШҜ. ШҜШұ ШІЫҢШұ ЪҶЪ© Щ…ЫҢвҖҢЪ©ЩҶЫҢЩ… Ъ©ЩҮ ШҜЩҲ ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢвҖҢ $x^3+y^3+z^3+xy+xz+yz$ ЩҲ $x^4+y^3+z^2-xyz$ ЩҶШіШЁШӘ ШЁЩҮ ШҜЩҲШұ $(x,y,z)$ ШҜЩҲШұЫҢ ЩҮШіШӘЩҶШҜ ЫҢШ§ Ш®ЫҢШұ.
sigma := Perm([[1, 2, 3]]):
f := x[1]^3 + x[2]^3 + x[3]^3 + x[1]*x[2] + x[1]*x[3] + x[2]*x[3];
eval(f, {seq(x[i] = x[sigma[i]], i = 1 .. 3)});
g := x[1]^4 - x[1]*x[2]*x[3] + x[2]^3 + x[3]^2;
eval(g, {seq(x[i] = x[sigma[i]], i = 1 .. 3)});
Ъ©ЩҮ Ш®ШұЩҲШ¬ЫҢвҖҢШ§Шҙ ШЁЩҮ ШҙЪ©Щ„ ШІЫҢШұ Щ…ЫҢвҖҢШҙЩҲШҜ.
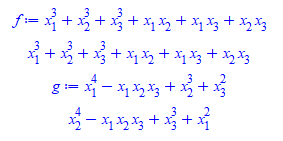
ЩҮЩ…Ш§ЩҶвҖҢЪҜЩҲЩҶЩҮ Ъ©ЩҮ Щ…ЫҢвҖҢШЁЫҢЩҶЫҢШҜ $(x,y,z)$ ЫҢЪ© ЩҶШ§ЩҲШұШҜШ§ ШЁШұШ§ЫҢ ЪҶЩҶШҜШ¬Щ…Щ„ЩҮвҖҢШ§ЫҢ ЫҢЪ©ЩҸЩ… Ш§ШіШӘ ЩҲЩ„ЫҢ ШЁШұШ§ЫҢ ШҜЩҲЩ…ЫҢ ЩҶЫҢШіШӘ.