رابطه ای جالب در دنباله فیبوناتچی

Question

سلام هنگام بررسی دنباله فیبوناتچی به رابطه ای جالب توجه و شاید هم جدید برای محاسبه جمله n ام آن رسیدم. نمی دانم فرمول نوشته شده قبلا توسط فردی دیگر محاسبه شده است یا نه ولی آن را اینجا برای شما به اشتراک می گذارم.

دنباله فیبوناتچی به شکل زیر است:

1 , 1 , 2 , 3 , 5 , 8 , 13 , ...

اگر $f_n$ جمله n ام این دنباله باشد و $ φ=\frac{1+\sqrt{5}}{2} $ آنگاه خواهیم داشت:

$ f_{n}=⌈\frac{φ^{2n-1}-1}{φ^{n-3}(φ^{4}-1)}⌉ $

در معادله بالا ⌈ ⌉ تابع سقف است.

یکی از مزیت های معادله بالا این است که میتوان شکلی از روند رشد دنباله فیبوناتچی حتی در قسمت های اعشاری یافت. به شکل زیر دقت کنید:

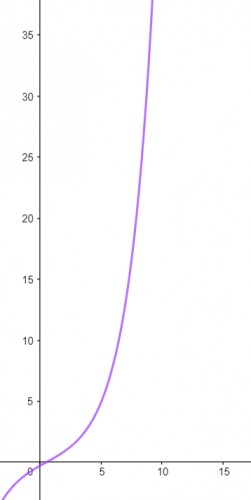
روند رشد تابع فیبوناتچی تقریبا به شکل بالاست.

آیا میتوانید فرمول ذکر شده را ثابت کنید؟

Comments

رابطه ای جالبی است تاکنون این رابطه را ندیدم هر چند به درستی آن مطمئن نیستم

---

سلام @amir7788 درستی این رابطه را من به اثبات رساندم

Answer 1

• داخل تابع سقف با$ x_{n} $ نشان می دهیم $$ x_{n} = \frac{ \varphi ^{2n-1}-1 }{ \varphi ^{n-3}( \varphi^4-1) } = \frac{ \varphi ^{2n-1}-1}{ \varphi ^{n-2}( \varphi+2) } $$ کافی است ثابت کنیم$ F_n-1<x_n<F_n $ نماد F برای دنباله شناخته شده فیبوناتچی در نظر گرفتیم.
• برای اثبات نامساوی سمت راست

$$x_n<F_n \Rightarrow \frac{ \varphi ^{2n-1}-1 }{ \varphi ^{n-2}( \varphi+2)} < \frac{ \varphi ^n-(-\varphi)^{-n}}{ \sqrt{5}} \Rightarrow \frac{ \sqrt{5} {\varphi} }{ \varphi+2} ( \varphi^{2n}- \varphi )< \varphi^{2n}-(-1)^n $$

• نامساوی فوق صحیح است چون تساوی $ \sqrt{5} {\varphi} = \varphi+2 $داریم.
• حال نامساوی سمت چپ نشان می دهیم $$F_n-1<x_n \Rightarrow \frac{ \varphi ^n-(- \varphi)^{-n}-\sqrt5}{ \sqrt{5}}< \frac{ \varphi ^{2n-1}-1 }{ \varphi ^{n-2}( \varphi+2)} $$ داریم $$ \varphi ^{2n}-(-1)^{-n}-\sqrt5\varphi^n< \frac{\sqrt5\varphi} {\varphi+2}(\varphi ^{2n}-\varphi) $$
• بنابراین داریم

$$g(n) =\sqrt5\varphi^n> \varphi- (-1)^n $$

• تابع gصعودی و $ g(1)>\sqrt5+1 $در نتیجه نامساوی فوق هم بر قرار است.