برای بدست آوردن این مجموع راه های زیادی وجود دارد . ولی از آنجا که شما این سوال را در مقطع هشتم یا نهم پرسیده اید پس بنده در اینجا راه حلی در سطح معلومات یک دانش آموز هشتم یا نهم می آورم .
ابتدا مجموع $ \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + ...$ را بدست می آوریم . یک مربع $1 \times 1$ در نظر بگیرید . این مربع را به $2$ قسمت مساوی تقسیم نمایید . نصف مربع را به رنگ زرد در می آوریم ( به شکل زیر نگاه کنید ) . این قسمت زرد رنگ در شکل نمایانگر کسر $ \frac{1}{2} $ است . حال نصف دیگر مربع را که رنگ نکرده ایم را به $2$ قسمت مساوی تقسیم می کنیم و نصف آن را به رنگ قرمز در می آوریم . این قسمت قرمز رنگ نمایانگر کسر $ \frac{1}{4} $ است . مجددا قسمتی را که هنوز رنگ نشده است را به $2$ قسمت مساوی تقسیم می کنیم . و نصف آن را به رنگ آبی در می آوریم . این قسمت آبی رنگ نمایانگر کسر $ \frac{1}{8} $ است . و این کار را ادامه می دهیم و به شکل زیر می رسیم :
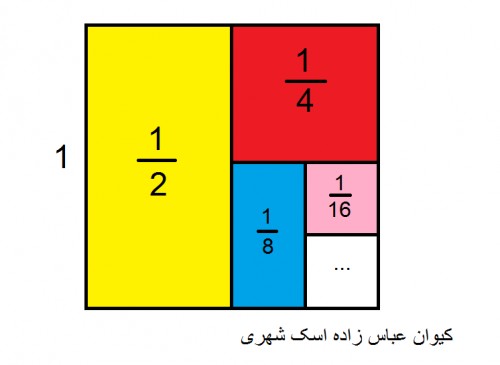
چون مجموع $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + ...$ تا بی نهایت می رود پس تقسیمات بالا را در مربع تا بی نهایت ادامه می دهیم . و این کار باعث رنگ شدن کل مربع $1 \times 1$ می شود که $1$ واحد کامل است . بنابراین :
$$\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + ... = 1$$
حال به طرفین تساوی بالا $1$ واحد اضافه می کنیم که خواهیم داشت :
$$1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + ... = 2$$