یک مستطیل ۵ در ۷ داریم که دو سه گوش از آن بریده شده است. با چند برش می توان این شکل را به یک مستطیل جدید تبدیل کرد؟

Question

شکل زیر را در نظر بگیرید. با چند برش مستقیم، و با کنار هم قرار دادن قطعات ایجادشده، می‌توان یک مستطیل ساخت؟

با برش‌های افقی و قائم موفق نشدم، به نظرم برش‌های مایل و حداقل یکی عمود بر قسمت مایل باید انجام شود.

Comments

@amir7788  احتمالا حداقل برش را می خواهید؟ چون اگر تمام خطوط افقی و عمودی را برش دهید آنگاه $33$ تا مربع می توانید داشته باشید که با اینها می توان مستطیل 3×11 درست کرد.

---

@Elyasi حداقل برش بهتر است اما با اختلاف 1 یا 2 برش بیشتر هم ایرادی نداره.

Answer 1

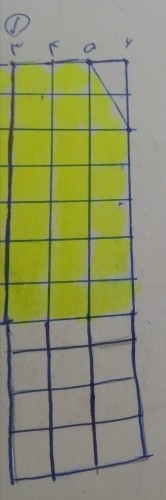
به نام خدا.

خطوط افقی را از بالا به پایین و خطوط عمودی را از چپ به راست به ترتیب شماره گذاری می کنیم.

مستطیل$2×1$ سمت چپ پایین، کامل کننده مستطیل $2×1$ بالا سمت راست است. حال حالت بندی می کنیم:

ردیف اول شامل $5$ خانه داشته باشد.

در این صورت حتی اگر تمام مربع ها تک تک قابلیت جابه جا شدن داشته باشند، باز هم نمی توان مستطیل درست کرد.

ردیف اول شامل$4$ خانه باشد.

در این صورت اگر تمام خانه های ستون اول تک تک قابل جابه جا شدن داشته باشند، باز هم نمی توان مستطیل درست کرد. زیرا $5$ مربع تنها یک ردیف چهار تایی با یک ردیف یکی می توانند تشکیل دهند.

ردیف اول شامل$3$ خانه باشد.

این حالت امکان دارد. به این صورت که خطوط افقی $4$ و $6$ را ببریم و سپس خطوط عمودی $2$ و $3$ را برش می دهیم.

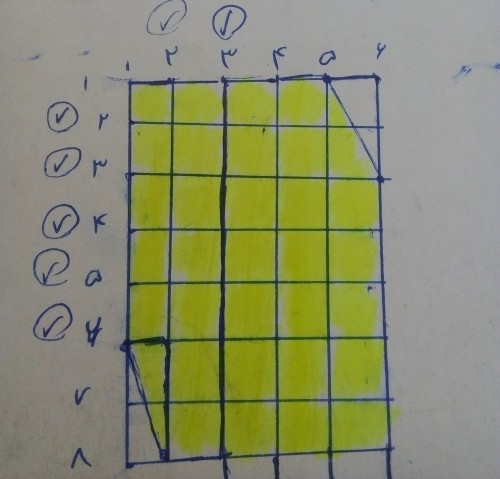مستطیل کامل کننده را بالا سمت راست می گذاریم تا مستطیل دیگر را کامل کنند.‌ حال مستطیل که بین دو خط عمودی $3,6$ و دو خط افقی $1,8$ است را ثابت می گیریم. سپس با $2$ مستطیل $1×3$ و سه مستطیل$1×2$ باقی مانده«منظور از مستطیل های باقیمانده، مستطیل هایی است که بین دو خط عمودی به شماره $1,3$ وجود دارند.» یک مستطیل$4×3$ درست می کنیم. به این صورت که دو مستطیل $1×3$ را به صورت افقی زیر هم و در زیر مستطیل ثابت می گذاریم. حال سه مستطیل $1×2$ را به صورت عمودی زیر مستطیل $1×3$ می گذاریم. شکل زیر 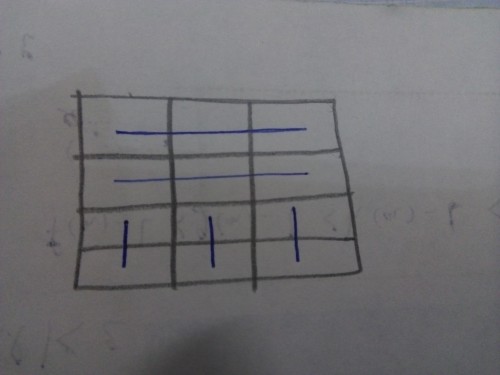در این صورت یک مستطیل $11×3$ داریم. پس با $4$ برش می توان یک مستطیل درست کرد.

Comments

@amir7788 پاسخ را ویرایش کردم. فکر کنم از این کمتر نشود.

---

@Elyas1 بنظرم  5 برش باشه؟

---

@amir7788 دو خط افقی و دو خط عمودی را برش دادیم. خط پنجم چرا داشته باشیم؟

---

@Elyas1  سه تا افقی سومی برای مثلث می باشه. برش های افقی 3، 5 و 6  به انداز 2 واحد یا دو خانه دارید

---

@amir7788 شما درست می فرمایید. ولی من برش های افقی 4 و 6 را درنظر گرفتم. به جای اینکه 3,5,6 را ببریم، خطوط 4,6 را ببریم بهتر است. چون تعداد برش ها کمتر می شود.

Answer 2

• شیوه اول از@Elyas1 در شکل زیر آوردم با 4 برش به 6 قطعه تقسیم می کنیم

• شیوه دوم با 4 برش به 5 قطعه مطابق شکل زیر تفکیک می کنیم.

• این شیوه همان راهنمایی بود که در متن پرسش گفتم چون قبلا دیده بودم اما فراموش کردم. به احتمال زیاد با این شیوه با برش کمتر از 4 احتمالا با 3 برش می توانید به جواب برسید. دوستان می توانند از این شیوه ایده بگیرند برای برش های کمتر.