ШЁЩҮ ЩҶШ§Щ… Ш®ШҜШ§.
Щ…ШӘЩҶ ШІЫҢШұ Ш§ШІ Ъ©ШӘШ§ШЁ ШұЩҲШҙ ЩҮШ§ЫҢ Ш¬ШЁШұ ЩҶЩҲШҙШӘЩҮ ЩҫШұЩҲЫҢШІ ШҙЩҮШұЫҢШ§ШұЫҢ Ш¬Щ„ШҜ ШҜЩҲЩ… ШөЩҒШӯЩҮ$428$ ЪҜШұЩҒШӘЩҮ ШҙШҜЩҮ Ш§ШіШӘ:
В« Ш§ШІ ЩҮЩҶШҜШіЩҮ Щ…ЫҢ ШҜШ§ЩҶЫҢЩ… Ъ©ЩҮ Ш§ЪҜШұ Ш®Ш·ЫҢ Щ…Ш«Щ„ $AB_1$ШҢ Щ…ЩҶШӯЩҶЫҢ $(C)$ ШұШ§ ШҜШұ ШҜЩҲ ЩҶЩӮШ·ЩҮ$A$ ЩҲ $B_1$ ЩӮШ·Ш№ Ъ©ЩҶШҜ(ШҙЪ©Щ„ $184$)ШҢ ЩҲЩӮШӘЫҢ Ъ©ЩҮ ЩҶЩӮШ·ЩҮ $B_1$ ШұЩҲЫҢ Щ…ЩҶШӯЩҶЫҢ $C$ ШЁЩҮ Ш·ШұЩҒ
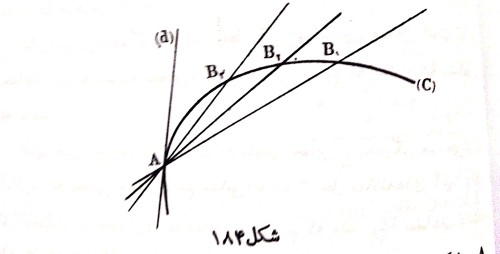
ЩҶЩӮШ·ЩҮ $A$ Щ…ЫҢЩ„ Ъ©ЩҶШҜШҢ Ш®Ш· $AB_1$ ШЁЩҮ Ш·ШұЩҒ Щ…Щ…Ш§Ші $d$ Щ…ЫҢЩ„ Ш®ЩҲШ§ЩҮШҜ Ъ©ШұШҜ. ШЁЩҶШ§ШЁШұШ§ЫҢЩҶ Ш®Ш· Щ…Щ…Ш§Ші ШЁШұ Щ…ЩҶШӯЩҶЫҢ ШұШ§ Щ…ЫҢ ШӘЩҲШ§ЩҶ Ш®Ш· ЩӮШ§Ш·Ш№ЫҢ ШҜШ§ЩҶШіШӘ Ъ©ЩҮ ШҜЩҲ ЩҶЩӮШ·ЩҮ ШЁШұШ®ЩҲШұШҜ ШўЩҶ ШЁШ§ Щ…ЩҶШӯЩҶЫҢ ШЁШұ ЩҮЩ… Щ…ЩҶШ·ШЁЩӮ ШҙШҜЩҮ ШЁШ§ШҙШҜ.
Щ…ЩҶШӯЩҶЫҢ $C$ ЩҲ ЩҶЩӮШ·ЩҮ $M$ ШұШ§ ШҜШұ ЩҶШёШұ Щ…ЫҢЪҜЫҢШұЫҢЩ…(ШҙЪ©Щ„ $185$). Ш®Ш·ЫҢ Ъ©ЩҮ Ш§ШІ ЩҶЩӮШ·ЩҮ$M$ Ш№ШЁЩҲШұ Ъ©ЩҶШҜШҢ Щ…Щ…Ъ©ЩҶ Ш§ШіШӘ Щ…ЩҶШӯЩҶЫҢ ШұШ§ Щ…Ш«Щ„Ш§ ШҜШұ ШҜЩҲ ЩҶЩӮШ·ЩҮ$A$ ЩҲ $B$ ЩӮШ·Ш№ Ъ©ЩҶШҜШҢ Ш§ЪҜШұ Щ…Ш№Ш§ШҜЩ„ЩҮ Щ…ЩҶШӯЩҶЫҢ $C$ ШұШ§ ШЁШ§ Щ…Ш№Ш§ШҜЩ„ЩҮ Ш®Ш·ЫҢ Ъ©ЩҮ Ш§ШІ ЩҶЩӮШ·ЩҮ$M$ Щ…ЫҢ ЪҜШ°ШұШҜШҢ ШЁЩҮ Ш№ЩҶЩҲШ§ЩҶ ЫҢЪ© ШҜШіШӘЪҜШ§ЩҮ ШҜЩҲ Щ…Ш№Ш§ШҜЩ„ЩҮ ШҜЩҲ Щ…Ш¬ЩҮЩҲЩ„ЫҢ ШҜШұ ЩҶШёШұ ШЁЪҜЫҢШұЫҢЩ…ШҢ ШЁШ§ ШӯШ°ЩҒ ЫҢЪ©ЫҢ Ш§ШІ Щ…Ш¬ЩҮЩҲЩ„ЩҮШ§ЫҢ $x,y$ ШЁЫҢЩҶ ШўЩҶЩҮШ§ШҢ ШҜШұ ЩҲШ¶Ш№ Щ…ЩҒШұЩҲШ¶ ШЁЩҮ ЫҢЪ© Щ…Ш№Ш§ШҜЩ„ЩҮ ШҜШұШ¬ЩҮ ШҜЩҲЩ… Щ…ЫҢ ШұШіЫҢЩ… Ъ©ЩҮ ШҜШұ ШӯШ§Щ„ШӘ Ш§ЩҲЩ„ ШҜЩҲ ШұЫҢШҙЩҮ ШӯЩӮЫҢЩӮЫҢШҢ ШҜШұ ШӯШ§Щ„ШӘ ШҜЩҲЩ… ШҜЩҲ ШұЫҢШҙЩҮ Щ…ШіШ§ЩҲЫҢ( ЫҢЪ© ШұЫҢШҙЩҮ Щ…Ш¶Ш§Ш№ЩҒ) ЩҲ ШҜШұ ШӯШ§Щ„ШӘ ШіЩҲЩ… ШҜЩҲ ШұЫҢШҙЩҮ Щ…ЩҲЩҮЩҲЩ…ЫҢ ШҜШ§ШұШҜ.
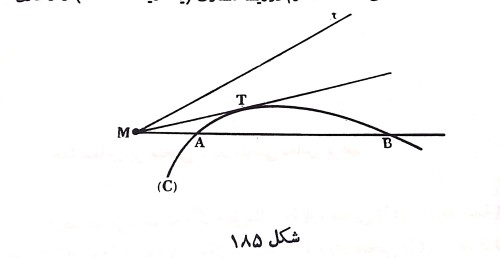
ШЁЩҶШ§ШЁШұШ§ЫҢЩҶ Щ…ЫҢ ШӘЩҲШ§ЩҶ ЪҜЩҒШӘ: ЫҢЪ© Ш®Ш· ЩҲЩӮШӘЫҢ ШЁШұ Щ…ЩҶШӯЩҶЫҢ Щ…Щ…Ш§Ші Ш§ШіШӘ Ъ©ЩҮ Ш§ШІ ШӯЩ„ Щ…Ш№Ш§ШҜЩ„ЩҮ ЫҢ ШўЩҶ ШЁШ§ Щ…Ш№Ш§ШҜЩ„ЩҮ ЫҢ Щ…ЩҶШӯЩҶЫҢШҢ ШЁЩҮ Щ…Ш№Ш§ШҜЩ„ЩҮвҖҢШ§ЫҢ ШЁШұШіЫҢЩ… Ъ©ЩҮ ЫҢЪ© ШұЫҢШҙЩҮ Щ…Ш¶Ш§Ш№ЩҒ ШҜШ§ШҙШӘЩҮ ШЁШ§ШҙШҜ.
ШҙШЁЫҢЩҮ ЩҮЩ…ЫҢЩҶ ШӘШ№ШұЫҢЩҒ ШұШ§ ШҜШұ Щ…ЩҲШұШҜ ШҜЩҲ Щ…ЩҶШӯЩҶЫҢ Щ…Щ…Ш§Ші ШЁШұ ЫҢЪ©ШҜЫҢЪҜШұ ЩҮЩ…ШҢ Щ…ЫҢ ШӘЩҲШ§ЩҶ ЩӮШЁЩҲЩ„ Ъ©ШұШҜ: ШҜЩҲ Щ…ЩҶШӯЩҶЫҢ ЩҲЩӮШӘЫҢ ШЁШұ ЩҮЩ… Щ…Щ…Ш§Ші Ш§ЩҶШҜ Ъ©ЩҮ Ш§ШІ ШӯЩ„ Щ…Ш№Ш§ШҜЩ„ЩҮ ЩҮШ§ЫҢ ШўЩҶЩҮШ§ ШЁШ§ ЩҮЩ…( Щ…Ш«Щ„ ШҜЩҲ Щ…Ш№Ш§ШҜЩ„ЩҮ ШҜЩҲ Щ…Ш¬ЩҮЩҲЩ„ЫҢ)ШҢ ШЁЩҮ Щ…Ш№Ш§ШҜЩ„ЩҮ Ш§ЫҢ ШЁШұШіЫҢЩ… Ъ©ЩҮ ЫҢЪ© ШұЫҢШҙЩҮ Щ…Ш¶Ш§Ш№ЩҒ ШҜШ§ШҙШӘЩҮ ШЁШ§ШҙШҜ.В»