جواب بهینه پارتو را توضیح دهید؟

Question

لطفا جواب بهینه پارتو را $(Pareto \ optimal \ solution)$ در برنامه سازی چند هدفه,شرح دهید.

Answer 1

در زندگی ناچار به تصمیم گیری، انتخاب و جستجو برای سازش و توافق هستیم. مشکلی که در این‌جا وجود دارد (حداقل به صورت جزیی) ناسازگاری اهداف موجود با هدف های مختلف ما هستند. مسئله بهینه سازی چند هدفه معمولی $ (MOP) $ به شکل زیر نوشته می شود:

$\min f(x) \qquad \qquad \qquad \qquad \qquad \qquad \qquad $

$s.t \in X \qquad \qquad \qquad \qquad \qquad \qquad \qquad$

و در آن $X\subseteq\mathbb{R}^{n}$ و $X \neq \varnothing $ و هم‌چنین$f(x) = {({f_1},{f_2},...,{f_k})^T}(x):\,\,X \to \,{R^k}$ یک تابع بردار مقدار است. که الزاما بردارها با همدیگه سزاگار نیستند و هم‌چنین $\vec{x}=(x_1,x_2,\ldots,x_k)$ بردار متغییرهای تصمیم است و $f_i : \mathbb{R}^n \to \mathbb{R},i = 1 ,\ldots,k$ نشان دهنده تابع هدف $i$ام است. و منظور از $min$ در بالا این است که تمام توابع هدف به طور هم‌زمان کمینه می‌شوند. مثال زیر می‌تواند یک نمونه خوب از یک بردار چند هدفه باشد که اهداف با هم سازگار نیستند :

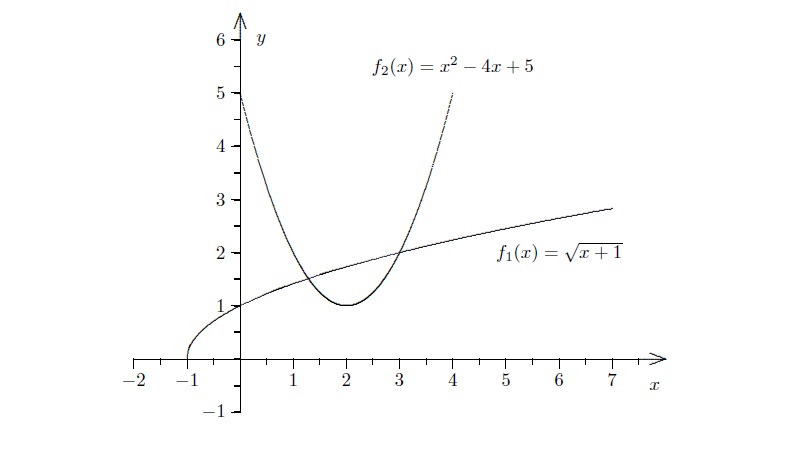
دو تابع $f_1(x) = \sqrt{x + 1} $ و $f_2(x) = x^2 - 4x +5$ در نظر گرفته شود. در این مثال هدف این است که این دو تابع به طور هم‌زمان نسبت به متغییر نامنفی $x$ کمینه شوند. در واقع به دنبال حل مسئله بهینه‌سازی \begin{align} \quad \min f(x) = (f_1(x) , f_2(x))\ s.t x \in \mathbb{R}_{\geq 0} \end{align} می‌باشد. هر دو تابع در شکل زیر رسم شده‌اند. حال سوالی که پیش می‌آید این است که، کمینه کننده‌ها کدام هستند؟

با توجه به شکل مشخص است که مقادیر $f_1(0) = 1$ و $f_2(2) = 1$ ، به ترتیب جواب‌های یکتای کمینه‌سازی برای توابع $f_1$ و $f_2$ روی مجموعه $X= \lbrace x \in \mathbb{R} : x \geq 0 \rbrace $ می‌باشند. مشاهده شد که هر کدام از توابع در یک نقطه متمایز از هم کمینه شدند و این یعنی این‌که در یک نقطه و به طور هم‌زمان بهینه نمی‌شوند. حال سوال این است که در مثال بالا کدام نقطه جواب مسئله یعنی $0 $یا 2 است؟ کدام جواب بیشتر به کار می‌آید؟

از آنجا که اکثرا اهداف با هم‌دیگر متناقض هستند، پیدا کردن یک جواب بهینه که به‌طور هم‌زمان تمام توابع را کمینه کند، تقریبا غیرممکن است. با این حال می‌توان مجموعه‌ای از جواب‌ها را یافت که بهترین تعامل را بین اهداف برقرار کند به طوری‌که بهبود نمی‌یابند مگر این‌که سبب بدتر شدن اهداف دیگر شود. در ادامه تعاریفی بیان می‌شود که باعث می‌شود این موضوع بیشتر روشن شود. خب در برخی مثال ها به جای اینکه در فضای تصمیم گیری دنبال جواب بگردن در فضای هدف جواب بهینه رو پیدا می‌کند و با استفاده از معکوس تابع جواب را در فضای تصمیم نیز بیان می‌کنند؛

کارا (بهینه پارتو): در مسئله چندهدفه به جواب شدنی $x^* \in X$ کارا یا بهینه پارتو گویند هر گاه:

$\nexists x \in X s.t f(x) \leq f(x^*) \qquad \qquad \qquad \qquad \qquad \qquad $

غیرغالب: اگر $x^* \in X$ کارا باشد، آن‌گاه $f(x^*) \in f(X)$ را غیرغالب گویند.

منظور از غیرغالب بودن این است که هیچ چیز نمی‌تواند بر آن غلبه کند، که در اینجا به این معنی است که هیچ مقداری کم‌تر از آن وجود ندارد.

مجموعه تمام جواب‌های کارای $x^* \in X$ را با $X_E$ نشان می‌دهند و مجموعه کارایی گویند هم‌چنین مجموعه تمام نقاط غیرغالب $y^* = f(x^*)$ را با $Y_N$ نشان داده و آن ‌را مجموعه غیرغالب گویند.

در ادامه تعاریفی دیگر از کارا بودن بیان شده است که با هم‌دیگر معادل هستند: $x^*$ کارا است اگر و فقط اگر

1. هیچ $x \in X$ وجود نداشته باشد به طوری‌که به ازای همه $i = 1 , \ldots , k $ ، $f_i(x) \leq f_i(x^) $ ،و هم‌چنین به ازای بعضی از $j \in \lbrace 1 , \ldots , k \rbrace$ ، $f_j(x) < f_j(x^)$ برقرار باشد.

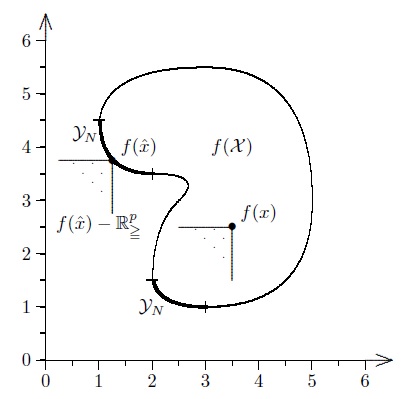
2. $\quad \qquad \qquad \quad \quad \nexists x \in X \ s.t \ f(x) - f(x^*) \in -\mathbb{R}^k_{\geqq} - \lbrace 0 \rbrace $

3. $ \qquad \qquad \forall x \in X : f(x) - f(x^*) \in \mathbb{R}^k - \lbrace - \mathbb{R}^p_{\geqq} - \lbrace 0 \rbrace \rbrace$

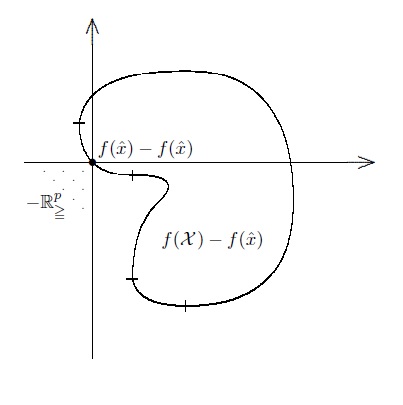
   در شکل زیر معادل تعریف هندسی $1$ و در شکل بعدیش معادل هندسی تعریف $2$ و $3$ آورده شده است.