ШЁЩҶШ§Щ… Ш®ШҜШ§ЩҲЩҶШҜ ШЁШ®ШҙЩҶШҜЩҮ ЩҲ Щ…ЩҮШұШЁШ§ЩҶ
ЩҫШұШіШҙ:
ШӘШ№ШҜШ§ШҜ ШұЫҢШҙЩҮвҖҢЩҮШ§ЫҢ Щ…Ш«ШЁШӘ ЩҲ Щ…ЩҶЩҒЫҢ ШӘШ§ШЁШ№
$f(x)=3^{2}-e^{x} $
ШұШ§ ШЁШ§ Ъ©Щ…Ъ© ШӘШ№ЫҢЫҢЩҶ Ш№Щ„Ш§Щ…ШӘ ЩҫЫҢШҜШ§ Ъ©ШұШҜЩҮ ЩҲ ШЁШұШ§ЫҢ ЩҮШұ ШұЫҢШҙЩҮ ЫҢЪ© ШЁШ§ШІЩҮвҖҢЫҢ Ш¬ШҜШ§ Ъ©ЩҶЩҶШҜЩҮ Ш§ШұШ§ШҰЩҮ Ъ©ЩҶЫҢШҜ.
ЩҫШ§ШіШ®:
Ш§ЪҜШұ Ш§ШІ Ш§ЫҢЩҶ ШӘШ§ШЁШ№ ШіЩҮ ШЁШ§Шұ Щ…ШҙШӘЩӮ ШЁЪҜЫҢШұЫҢЩ… ШЁЩҮ ШӘШ§ШЁШ№ ШіШ§ШҜЩҮвҖҢШӘШұЩҗ $-e^{x}$ Щ…ЫҢвҖҢШұШіЫҢЩ… Ъ©ЩҮ ЩҮЩ…ЩҲШ§ШұЩҮ Щ…ЩҶЩҒЫҢ Ш§ШіШӘ. ЪҶЩҲЩҶ ШӘШ§ШЁШ№ $e^{x}$ ЩҮЩ…ЩҲШ§ШұЩҮ Щ…Ш«ШЁШӘ Ш§ШіШӘ. ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ ЩҮШҜЩҒ Щ…ШіШ§Щ„ЩҮ Ъ©ЩҮ ЫҢШ§ЩҒШӘЩҶ ШӘШ№ШҜШ§ШҜ ШұЫҢШҙЩҮвҖҢЩҮШ§ШҢ Щ…ШӯШҜЩҲШҜЩҮвҖҢЫҢ ШўЩҶвҖҢЩҮШ§ ЩҲ Ш№Щ„Ш§Щ…ШӘ ШўЩҶвҖҢЩҮШ§ШіШӘШҢ Ш¬ШҜЩҲЩ„ ШІЫҢШұ ШұШіЩ… Щ…ЫҢвҖҢЪ©ЩҶЫҢЩ…:
$$\begin{array}{c|ccc}
x & & \\\hline
f(x)=3x^2-e^x & & & \\\hline
f'(x)=6x-e^x & & & \\\hline
f''(x)=6-e^x & & \searrow & \\\hline
f^{(3)}(x)=-e^x & & - &
\end{array}$$
ШӘЩҲШ¬ЩҮ Ъ©ЩҶЫҢШҜ Ъ©ЩҮ ШҜШұ ШҜЩҲ ШіШ·Шұ ШўШ®Шұ Ш¬ШҜЩҲЩ„ Ш§ЫҢЩҶ ЪҜЩҲЩҶЩҮ Ш№Щ…Щ„ Ъ©ШұШҜЫҢЩ… Ъ©ЩҮ ЪҶЩҲЩҶ $ f^{(3)}< 0 $ ЩҫШі $ f'' $ Ъ©Ш§ЩҮШҙЫҢ Ш§Ъ©ЫҢШҜ ( Ш§Ъ©ЫҢШҜШ§ ЩҶШІЩҲЩ„ЫҢ) Ш§ШіШӘ. ЫҢЪ© ШӘШ§ШЁШ№ ШҜШұ ШЁШ§ШІЩҮвҖҢШ§ЫҢ Ъ©ЩҮ ЫҢЪ©ЩҶЩҲШ§ЫҢ Ш§Ъ©ЫҢШҜ Ш§ШіШӘ ШӯШҜШ§Ъ©Ш«Шұ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶШҜ ЫҢЪ© ШұЫҢШҙЩҮ ШҜШ§ШҙШӘЩҮ ШЁШ§ШҙШҜ. Ш§ШЁШӘШҜШ§ Ш§ШІ ШӯШҜ ШҜШұ ШЁЫҢЩҶЩҮШ§ЫҢШӘвҖҢЩҮШ§ Ш§ШіШӘЩҒШ§ШҜЩҮ Щ…ЫҢвҖҢЪ©ЩҶЫҢЩ…. ШІЫҢШұШ§ Ш§ЪҜШұ ШҜШұ ЩҮШұ ШҜЩҲ ШЁЫҢЩҶЩҮШ§ЫҢШӘ ЫҢЪ© Ш№Щ„Ш§Щ…ШӘ ШҜШ§ШҙШӘЩҮ ШЁШ§ШҙШҜШҢ ШҜШұ ЩҶШӘЫҢШ¬ЩҮ ШҜШұ Ъ©Щ„ $\mathbb{R} $ ЫҢЪ© Ш№Щ„Ш§Щ…ШӘ ШҜШ§ШұШҜ ЩҲ ЩҮШұЪҜШІ Ш§ШІ ШөЩҒШұ Ш№ШЁЩҲШұ ЩҶШ®ЩҲШ§ЩҮШҜ Ъ©ШұШҜ.
$$\lim_{x \to -\infty}(6-e^{x})=6-\lim_{x \to-\infty}e^{x}=6-0=6>0$$
ЩҲ
$$\lim_{x \to +\infty}(6-e^{x})=6-\lim_{x \to +\infty}e^{x}=6-\infty=-\infty< 0$$
ЩҫШі $ f^2 $ ЫҢЪ© ШұЫҢШҙЩҮ ШҜШ§ШұШҜШҢ ШўЩҶвҖҢШұШ§ $ x_{0} $ Щ…ЫҢвҖҢЩҶШ§Щ…ЫҢЩ…. ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Ш§Ш·Щ„Ш§Ш№Ш§ШӘ ШЁШ§Щ„Ш§ Ш¬ШҜЩҲЩ„ ШӘШ№ЫҢЫҢЩҶ Ш№Щ„Ш§Щ…ШӘ ШұШ§ ШұШіЩ… Щ…ЫҢвҖҢЪ©ЩҶЫҢЩ…:

ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Ш§ЫҢЩҶЪ©ЩҮ ЫҢЪ© ШұЫҢШҙЩҮ ШҜШ§ШұЫҢЩ… Щ…ЩҲЩӮШӘШ§ Ш§ШІ ЫҢШ§ЩҒШӘЩҶ ШЁШ§ШІЩҮ ШөШұЩҒ ЩҶШёШұ Щ…ЫҢвҖҢЪ©ЩҶЫҢЩ…. Ш§Ъ©ЩҶЩҲЩҶ Щ…ЩӮШҜШ§Шұ $ f^1 $ ШұШ§ ШҜШұ ШЁЫҢЩҶЩҮШ§ЫҢШӘвҖҢЩҮШ§ ЪҶЪ© Щ…ЫҢвҖҢЪ©ЩҶЫҢЩ….
$$\lim_{x \to -\infty}(6x-e^{x})=\lim_{x \to-\infty}6x-\lim_{x \to -\infty}e^{x}=-\infty-0=-\infty< 0$$
ЩҲ
$$\lim_{x \to +\infty}(6x-e^{x})=\lim_{x \to +\infty}6x-\lim_{x \to +\infty}e^{x}=-\infty< 0 $$
ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Ш§ЫҢЩҶЪ©ЩҮ ШұШҙШҜ ШӘШ§ШЁШ№ $e^{x}$ ШҜШұ ШЁЫҢЩҶЩҮШ§ЫҢШӘ ШіШұЫҢШ№вҖҢШӘШұ Ш§ШІ ШӘШ§ШЁШ№ $ 6x $ Ш§ШіШӘ ШЁЩҶШ§ШЁШұШ§ЫҢЩҶ ШӯШҜ ШӘШ§ШЁШ№ $ f^{1} $ ШҜШұ Щ…Ш«ШЁШӘ ШЁЫҢЩҶЩҮШ§ЫҢШӘШҢ ШЁШұШ§ШЁШұ Щ…ЩҶЩҒЫҢ ШЁЫҢЩҶЩҮШ§ЫҢШӘ Щ…ЫҢвҖҢШҙЩҲШҜ. ШЁШұШ§ЫҢ ШӘШ§ШЁШ№ $ f^1 $ ЫҢЪ©ЫҢ Ш§ШІ ЪҶЩҶШҜ ШӯШ§Щ„ШӘ ШІЫҢШұ ШұШ§ Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
Ш§ЪҜШұ
$ f^1 (x_0 )< 0 $
ШўЩҶвҖҢЪҜШ§ЩҮ ШӘШ§ШЁШ№ $ f^1 $ШҜШұ Ъ©Щ„ $ \mathbb{R} $ Щ…ЩҶЩҒЫҢ Ш®ЩҲШ§ЩҮШҜ ШЁЩҲШҜ.
Ш§ЪҜШұ
$ f^1 (x_0 )=0 $
ШўЩҶвҖҢЪҜШ§ЩҮ ЩҶЩӮШ·ЩҮвҖҢЫҢ $ x_0 $ ШӘЩҶЩҮШ§ ШұЫҢШҙЩҮвҖҢЫҢ ШӘШ§ШЁШ№ $ f^1 $ Ш®ЩҲШ§ЩҮШҜ ШЁЩҲШҜ.
Ш§ЪҜШұ
$ f^1 (x_0 )>0 $
ШўЩҶвҖҢЪҜШ§ЩҮШҢ ШӘШ§ШЁШ№ $ f^1 $ЫҢЪ© ШұЫҢШҙЩҮ ЩӮШЁЩ„ Ш§ШІ ($ x_0 $) ЩҲ ЫҢЪ© ШұЫҢШҙЩҮ ШЁШ№ШҜ Ш§ШІ ($ x_0 $ ) Ш®ЩҲШ§ЩҮШҜ ШҜШ§ШҙШӘ.
ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Ш§ЫҢЩҶЪ©ЩҮ Щ…ЩӮШҜШ§Шұ $ x_0 $ ШұШ§ ЩҶШҜШ§ШұЫҢЩ…ШҢ Ш§ШЁШӘШҜШ§ $ f^1 (x_0 )=0 $ ШұШ§ ШЁШұШұШіЫҢ Щ…ЫҢвҖҢЪ©ЩҶЫҢЩ…. ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Ш§ЫҢЩҶЪ©ЩҮ $ f^2 (x_0 )=0 $
ШҜШ§ШұЫҢЩ…:
$$f^2(x) = 0 \Rightarrow 6 - {e^x} = 0 \to 6 = {e^x}$$
ЩҲ
$$f^1(x) = 0 \Rightarrow 6x - {e^x} = 0 \to 6x = {e^x}$$
ШҜШұ ЩҶШӘЫҢШ¬ЩҮ:
$ 6 = 6x \Rightarrow x = 1$
ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Щ…ЩӮШҜШ§ШұЫҢ Ъ©ЩҮ ШЁШұШ§ЫҢ $ x $ ШЁШҜШіШӘ ШўЩҲШұШҜЫҢЩ… ШҜШ§ШұЫҢЩ…:
$$f^{2}(1)=6-e^{1}=6-2.7\simeq3.3>0 $$
( ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Ш§ЫҢЩҶЪ©ЩҮ Щ…Ш§ ШұЩҲШҙ ШұЫҢШҙЩҮвҖҢЫҢШ§ШЁЫҢ Ш№ШҜШҜЫҢ ШұШ§ Ъ©ЩҶШ§Шұ ЪҜШ°Ш§ШҙШӘЫҢЩ…ШҢ Ш¬Ш§ЫҢвҖҢЪҜШ°Ш§ШұЫҢ ШҜШұ ШұЩҲШ§ШЁШ· Щ…Ш¬Ш§ШІ Ш§ШіШӘ.) ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ ШұШ§ШЁШ·ЩҮвҖҢЫҢ ШЁШ§Щ„Ш§ Ш§ЪҜШұ $ f^1 (x_0 )=0 $ ШўЩҶвҖҢЪҜШ§ЩҮ ШЁШ§ЫҢШҜ ШҜШ§ШҙШӘЩҮ ШЁШ§ШҙЫҢЩ…: $ x_0=1 $.
Ш§ЪҜШұ $ x_0=1 $ ШўЩҶвҖҢЪҜШ§ЩҮ: $ f^2(x_0)=f^2(1)=3.3\neq 0 $ ЩҲ Ш§ЫҢЩҶ ШЁШ§ ЩҒШұШ¶ Щ…Ш§ ШҜШұ ШӘЩҶШ§ЩӮШ¶ Ш§ШіШӘ. ЩҫШі ЩҒШұШ¶ Ш®Щ„ЩҒ
$ ( f^1 (x_0)=0 ) $
ШЁШ§Ш·Щ„ Ш§ШіШӘ ЩҲ Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
$f^1 (x_0)\neq0$.
ШЁШұШ§ЫҢ ШЁШҜШіШӘ ШўЩҲШұШҜЩҶ ЫҢЪ© ШӘЩӮШұЫҢШЁ Ш§ЩҲЩ„ЫҢЩҮ Щ…ЩӮШҜШ§ШұЫҢ ШҜЩ„Ш®ЩҲШ§ЩҮ ШұШ§ ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ ШҙШұШ§ЫҢШ· Щ…ШіШҰЩ„ЩҮ ШӯШҜШі Щ…ЫҢвҖҢШІЩҶЫҢЩ… (Щ…Ш«Щ„Ш§: $ x=0 $) ШӘШ§ ШЁШЁЫҢЩҶЩ… Ъ©ЩҮ ШҜШұ ЪҶЩҮ ЩҒШ§ШөЩ„ЩҮвҖҢШ§ЫҢ ЩҶШіШЁШӘ ШЁЩҮ
$ x_0 $
ЩӮШұШ§Шұ ШҜШ§ШұШҜ. ШҜШ§ШұЫҢЩ…:
$${f^x}(0) = 6 - {e^0} = 5 > 0$$
ЩҲ
$${f^1}(0) = 6(0) - {e^0} = 0 - 1 = - 1 < 0$$
ШҜШұ ЩҶШӘЫҢШ¬ЩҮ:
$ x_{0}>0$
ШЁШ§ Ш§ЩҶШӘШ®Ш§ШЁ Ш№ШҜШҜ ШЁШ№ШҜЫҢ $ (x=2) $ ШҜШ§ШұЫҢЩ…:
$$
{f^2}(2) = 6 - {e^2} = 6 - 7.3 \simeq - 1.3 < 0$$
ЩҲ
$${f^1}(2) = 6(2) - {e^2} = 12 - 7.3 \simeq 4.7 > 0$$
ШҜШұ ЩҶШӘЫҢШ¬ЩҮ:
${x_0} < 2$
ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Щ…Ш«ШЁШӘ ШЁЩҲШҜЩҶ Щ…ЩӮШҜШ§Шұ $ f^{1}(2) $ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ ЩҶШӘЫҢШ¬ЩҮ ЪҜШұЩҒШӘ Ъ©ЩҮ ШӯШ§Щ„ШӘ ШіЩҲЩ… ШЁШұЩӮШұШ§Шұ Ш§ШіШӘШҢ ЩҫШі $ f^{1} $ ШҜЩҲ ШұЫҢШҙЩҮ ШҜШ§ШұШҜШҢ ШўЩҶвҖҢЩҮШ§ ШұШ§ $ x_{1} $ ЩҲ $ x_{2} $ Щ…ЫҢвҖҢЩҶШ§Щ…ЫҢЩ…. ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ ЩӮШіЩ…ШӘ (3) ШҜШ§ШұЫҢЩ…: $ x_{1}< x_{0}< x_{2} $ШҢ ШЁЩҮвҖҢШ№Щ„Ш§ЩҲЩҮ ЪҶЩҲЩҶ $ f^{1}(0)< 0 $ ЩҲ $ f^{1}(2)>0 $ ЩҫШі $ 0< x_{1}< x_{0}< x_{2}< 2 $. ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Ш§ЫҢЩҶ ШӘЩҲШ¶ЫҢШӯШ§ШӘ Ш¬ШҜЩҲЩ„ (3) ШІЫҢШұ ШұШ§ Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
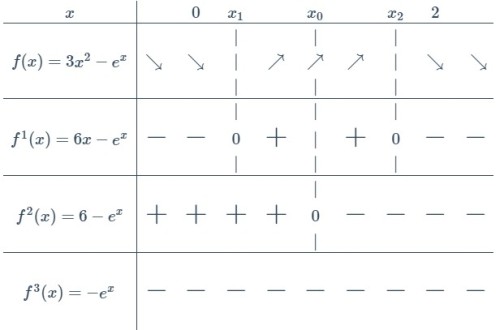
Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ ШӯШҜШі ШІШҜ Ъ©ЩҮ ЩҶШ®ШіШӘЫҢЩҶ ЪҜШ§Щ… ШЁШ№ШҜЫҢ ЪҶЫҢШіШӘ! Ш§Ъ©ЩҶЩҲЩҶ ШЁЩҮ ШЁШұШұШіЫҢ ШӯШҜ $ f(x) $ ШҜШұ ШЁЫҢЩҶЩҮШ§ЫҢШӘвҖҢЩҮШ§ Щ…ЫҢвҖҢЩҫШұШҜШ§ШІЫҢЩ….
$$\mathop {\lim }\limits_{x \to - \infty } (3{x^2} - {e^x}) = \mathop {\lim }\limits_{x \to - \infty } 3{x^2} - \mathop {\lim }\limits_{x \to - \infty } {e^x} = + \infty - 0 > 0$$
ЩҲ
$$\mathop {\lim }\limits_{x \to + \infty } (3{x^2} - {e^x}) = \mathop {\lim }\limits_{x \to +\infty } 3{x^2} - \mathop {\lim }\limits_{x \to +\infty } {e^x} = - \infty < 0$$
ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ ШӘШіШ§ЩҲЫҢ ШЁШ§Щ„Ш§ Ш¬ШҜЩҲЩ„(4) ШІЫҢШұ ШұШ§ Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
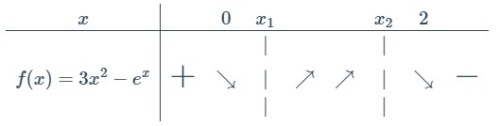
ШЁШ§ Ш§ШіШӘЩҒШ§ШҜЩҮ Ш§ШІ ЩҶЩӮШ·ЩҮвҖҢЩҮШ§ЫҢ Ъ©Щ…Ъ©ЫҢ Щ…ШұШӯЩ„ЩҮвҖҢЫҢ ЩӮШЁЩ„ ШҜШ§ШұЫҢЩ…: $f(0)=3(0)^{2}-e^{0}=-1< 0$.
ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Ш§ЫҢЩҶ ШӘШіШ§ЩҲЫҢ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶЫҢЩ… ЩҶШӘЫҢШ¬ЩҮ ШЁЪҜЫҢШұЫҢЩ… Ъ©ЩҮ ШӘШ§ШЁШ№
$f$
ШҜЩӮЫҢЩӮШ§ ЫҢЪ© ШұЫҢШҙЩҮ ШҜШұ $ (-\infty,x_{1}) $ ШҜШ§ШұШҜ Ъ©ЩҮ Ш§ШӘЩҒШ§ЩӮШ§ ШҜШұ ШЁШ§ШІЩҮвҖҢЫҢ
$ (-\infty,0) $
ЩӮШұШ§Шұ ШҜШ§ШұШҜ. ЩҫШі:
*ШӘШ№ШҜШ§ШҜ ШұЫҢШҙЩҮвҖҢЩҮШ§ЫҢ Щ…ЩҶЩҒЫҢ ШҜЩӮЫҢЩӮШ§ ЫҢЪ© Ш§ШіШӘ ЩҲ $(-\infty,0)$ ЫҢЪ© ШЁШ§ШІЩҮвҖҢЫҢ Ш¬ШҜШ§ Ъ©ЩҶЩҶШҜЩҮ ШЁШұШ§ЫҢ ШўЩҶ Ш§ШіШӘ.
ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ ШӘШіШ§ЩҲЫҢ $f(2)=3(2)^{2}-e^{2}=12-7.3>0$
ЩҲ Ш¬ШҜЩҲЩ„ ШЁШ§Щ„Ш§ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶЫҢЩ… ЩҶШӘЫҢШ¬ЩҮ ШЁЪҜЫҢШұЫҢЩ… Ъ©ЩҮ ШӘШ§ШЁШ№
$f$
ШҜЩӮЫҢЩӮШ§ ЫҢЪ© ШұЫҢШҙЩҮ ШЁЫҢЩҶ$ x_{1} $ ЩҲ $ x_{2} $ ЫҢЪ© ШұЫҢШҙЩҮ ШҜШұ
$ (x_{2},\infty)$
ШҜШ§ШұШҜ. (ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ ШұШ§ШЁШ·ЩҮвҖҢЫҢ
$ 0< f(2)< f(x_{2}) $
ШҜШ§ШұЫҢЩ…:
$ f(x_{2})>0 $)
ШЁЩҮвҖҢШ№Щ„Ш§ЩҲЩҮ Ш§ЫҢЩҶ ШұЫҢШҙЩҮ ШЁШ§ЫҢШҜ ШҜШұ ШЁШ§ШІЩҮвҖҢЫҢ
$ (2,+\infty) $
ШЁШ§ШҙШҜ. ШЁЩҶШ§ШЁШұШ§ЫҢЩҶ:
*** ШӘШ№ШҜШ§ШҜ ШұЫҢШҙЩҮвҖҢЩҮШ§ЫҢ Щ…Ш«ШЁШӘ ШҜЩӮЫҢЩӮШ§ ШҜЩҲ Ш§ШіШӘ ЩҲ $ (0,2) $ ЩҲ $ (2,\infty) $ ШҜЩҲ ШЁШ§ШІЩҮвҖҢЫҢ Ш¬ШҜШ§ Ъ©ЩҶЩҶШҜЩҮ ШЁШұШ§ЫҢ ШўЩҶвҖҢЩҮШ§ ЩҮШіШӘЩҶШҜ.**
ШӘШ°Ъ©Шұ: ШӘЩҶЩҮШ§ Щ…ШӯШ§ШіШЁЩҮвҖҢЩҮШ§ЫҢ ШұШ§ЫҢШ§ЩҶЩҮвҖҢШ§ЫҢ ЫҢШ§ Ш№ШҜШҜЫҢ Ъ©ЩҮ Ш§ЩҶШ¬Ш§Щ… ШҙШҜ Щ…ЩӮШ§ШҜЫҢШұ $ e^{1}$ ЩҲ $ e^{2}$ ШЁЩҲШҜЩҶШҜ Ъ©ЩҮ ШӯШӘЫҢ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ Ш§ШІ Ш¬ШҜЩҲЩ„вҖҢЩҮШ§ЫҢ Ш№ШҜШҜЫҢ ШўЩ…Ш§ШұЫҢ ЩҮЩ… ШўЩҶвҖҢЩҮШ§ ШұШ§ ШЁШҜШіШӘ ШўЩҲШұШҜ ЩҲ ШЁШұШ§ЫҢ Щ…ШӯШ§ШіШЁШ§ШӘ ШЁЩҮ Ш§ШЁШІШ§ШұЩҮШ§ЫҢ Щ…ШӯШ§ШіШЁШ§ШӘЫҢ Щ…ШӘЩҲШіЩ„ ЩҶШҙШҜ. ЩҫШі Щ…ШҙШ§ЩҮШҜЩҮ Ъ©ШұШҜЫҢШҜ Ъ©ЩҮ ШЁШұШ§ЫҢ Щ…ШӯШ§ШіШЁЩҮ ЩҮЩ… ЩҮШІЫҢЩҶЩҮвҖҢЫҢ ЪҶЩҶШҜШ§ЩҶЫҢ ЩҫШұШҜШ§Ш®ШӘ ЩҶЪ©ШұШҜЫҢЩ…! ШЁШ§ ШӘШҙЪ©Шұ Ш§ШІ Ш§ШіШӘШ§ШҜ Ш§Щ…ЫҢШұШӯШіЫҢЩҶ ШөШ§ШҜЩӮЫҢвҖҢЩ…ЩҶШҙ Ъ©ЩҮ ШҜШұ ШӯЩ„ ШҜЩӮЫҢЩӮ Ш§ЫҢЩҶ ШіЩҲШ§Щ„ ШұШ§ЩҮЩҶЩ…Ш§ЫҢ Щ…ЩҶ ШЁЩҲШҜЩҶШҜ.
