در واقع اگر ما مثلثی به طول وتر یک را در نظر بگیریم آنگاه طول ضلعها ی یک زاویه همان مقدار کسینوس یا سینوس آن زاویه می شوند
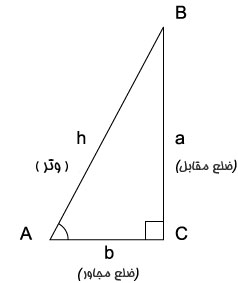
$$sin A = \frac{َBC}{AB}= \frac{BC}{1} =BC $$
$$cos A = \frac{َAC}{AB}= \frac{AC}{1} =AC $$
حال اگر مبدا مختصات را روی راس زاویه قرار دهیم به طوریکه یکی از محور ها بر یکی از ضلعها مماس شود آنگاه محور ها بیان کننده مقدار سینوس یا کسینوس می شوند
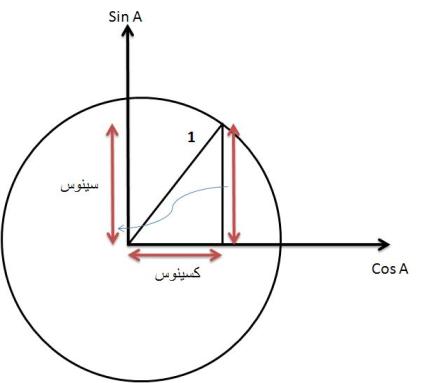
لذا باید شعاع دایره را $1$ بگیریم.
در جواب سوال دوم همانطور که خیلی کامل رضا نشون داد مقدار سینوس و کسینوس ربطی به شعاع دایره نداره اما اگر شعاع دایره را غیر از یک مثلا $ R $ بگیریم آنگاه محورها مقدار $R.sin A $ و $R.cos A $را نشان می دهند نه سینوس و کسینوس رو
چون در مثلث امکان نداره دو زاویه قائمه داشته باشیم بطور رسمی برای زاویه $90$ رابطه ای مانند زوایای حاده دیگر نداریم اما توجیهاتی وجود دارد که اتفاقا از واقعیت نشات می گیرندمثلا اگر زاویه به 90 نزدیک شود ضلع رو به رو هی بزرگ و ضلع مجاور کوچک می شود(وتر را ثابت بگیریم) در $90$ ضلع رو به رو و وتر یکی می شوند(پس نسبتشون $1$ میشه) و مجاور صفر میشه (پس نسبت مجاور به وتر برابر صفر است)