چگونه تقارن نسبت به مبدأ مختصات، محور $x$ها و محور $y$ها را تشخیص دهیم؟

Question

باسلام. این که می‌گوییم تابعی نسبت به مبدأ مختصات متقارن است و یا اینکه نسبت به محور $y$ها متقارن است و یا اینکه نسبت به محور $x$ها متقارن است، دقیقا به چه معنی است؟ من متوجه نمی‌شوم. ممنون می‌شوم به صورت ساده توضیح دهید. نمی‌دانم چگونه باید این تقارن‌ها را چک کنم تا بدانم برای تابعی که می‌دهند برقرار است یا خیر. باسپاس.

Answer 1

وقتی میگوییم نسبت به یک محور متقارن است یعنی نمودار نسبت به آن محور متقارن است مانند یک آینه مثلا تصویر زیر نمودار تابعی است که نسبت به محور $ y$ ها متقارن است.

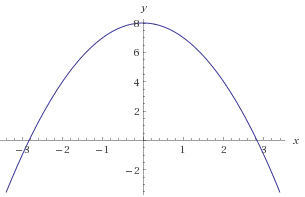
وقتی میگوییم نسبت به یک نقطه متقارن است(مثل مبدا مختصات) یعنی اگر هر نقطه روی نمودار را در نظر بگیریم و آن را به نقطه تقارن وصل کنیم و به همان فاصله( نقطه دلخواه انتخاب شده تا نقطه تقارن) ادامه دهیم باز نقطه ای از نمودار بدست آید مانند شکل زیر:

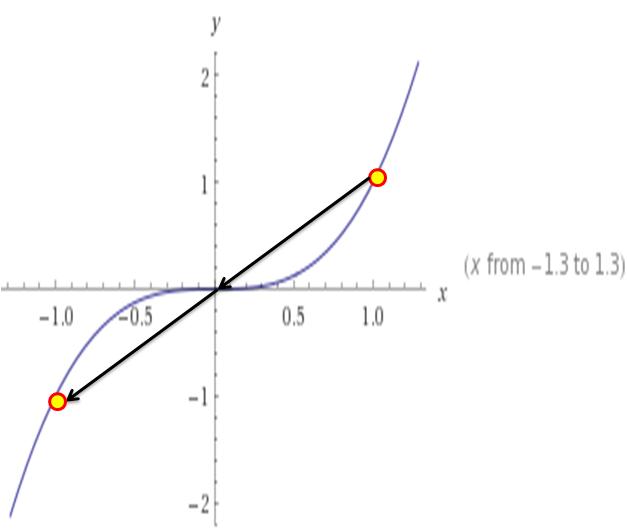
نحوه تشخیص:

اگر تابعی زوج باشد نمودار تابع نسبت به محور $ y$ ها متقارن است. ( زوج بودن یعنی اگر در ضابطه $ x $ را به $ -x $ تبدیل کنیم ضابطه تغییر نکند به عبارت دیگر$f(-x)=f(x) $)

اگر تابعی فرد باشد نمودار تابع نسبت به مبدا مختصات متقارن است. ( فرد بودن یعنی اگر در ضابطه $ x $ را به $ -x $ تبدیل کنیم ضابطه جدید قرینه ضابطه قبلی باشد به عبارت دیگر$f(-x)=-f(x) $)

دقت کنید که اگر نموداری نسبت به محور $x $ ها متقارن باشد آنگاه نمودار یک تابع نیست