قضيه ايي در مثلث متساوي الضلاع

Question

اثبات كنيد: چنانچه در از نقطه دلخواه درون مثلث متساوي الضلاع سه پاره خط به موازات سه ضلع رسم تا اضلاع مثلث را در سه نقطه قطع كند آنگاه مجموع پاره خط ها برابر ضلع مثلث متساوي الضلاع

Answer 1

ابتدا مثلث متساوي الضلاع $ABC$ را كشيده ونقطه دلخواه $m$ را درون آن قرار ميدهيم. و از نقطه $m$ سه پاره خط موازي ضلع هاي $AB,AC,BC$ رسم ميكنيم.!

همانطور كه از شكل پيداست سه ذوزنقه متساوي الساقين به وجود مي آيد .

بنابر اين :

$$\begin{cases}Ch'=nh \longrightarrow \triangle Cn'h' \cong \triangle mhn & \\ Bp=p'n'' \longrightarrow\triangle mp'n'' \cong \triangle Bnp &\end{cases}$$

حالا مثلث قائم الزاويه كه زاويه هاي($30,60$ )دارد رو در نظر بگير !!چه رابطه ايي بين وتر و اضلاع آن وجود دارد؟!! بيا ببينيم:

$$sin(30)= \frac{1}{2}$$

$$sin(60)= \frac{ \sqrt{3 } }{2}$$

بنابراين داريم:

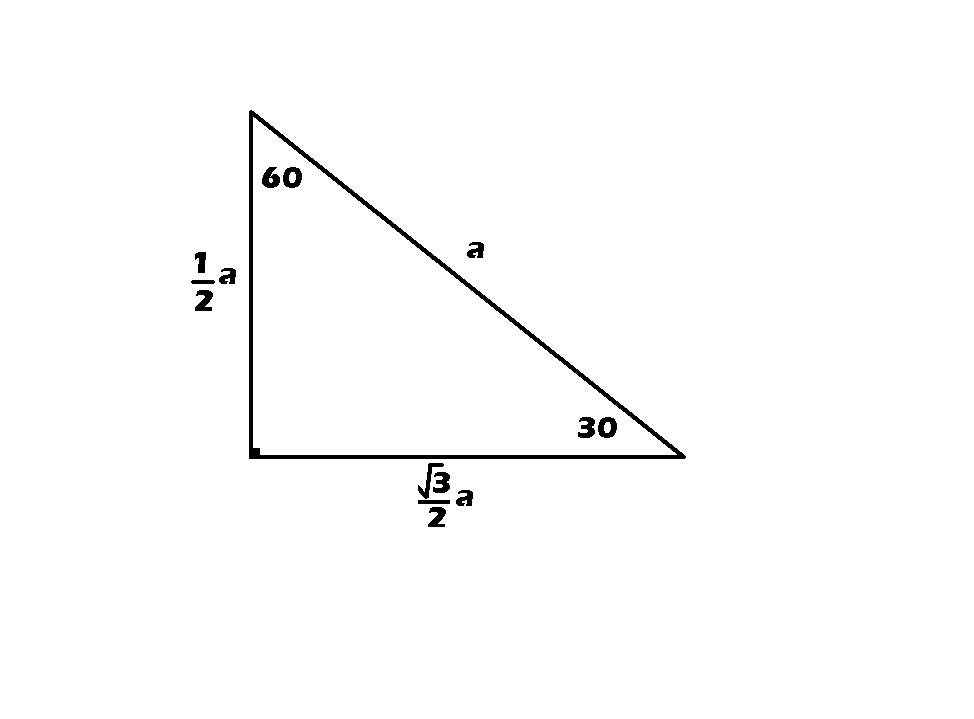
واز اين نتيجه ميگيريم كه:

$$\begin{cases}Ch'=nh= \frac{1}{2}nm \longrightarrow Ch'+nh=nm &\\Bp=p'n''= \frac{1}{2}Bn \longrightarrow Bp+ p'n''=mn'' & \end{cases}$$

ودر آخر اين سه رابطه رو در كنار هم قرار داده و جمع ميكنيم:

$$Ch'+nh=mn$$

$$Bp+ p'n''=Bn=mn''$$

$$hh'=mn'$$

$$mn+mn'+mn''=Ch'+hh'+nh+Bn$$

$$mn+mn'+mn''=BC=AC=AB$$

Answer 2