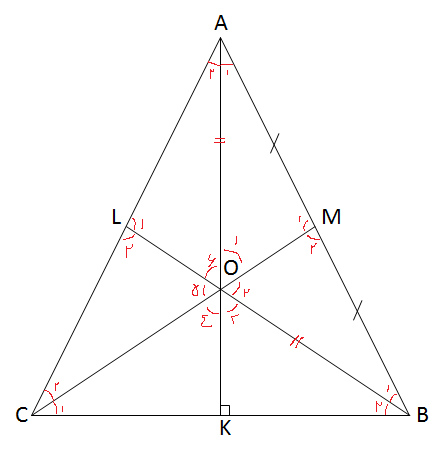
مثلث های AOM و BOM به دلیل سه ضلع برابرند و زاویه M1=M2=90
مثلثBOK هم به دلیل وتر و یک زاویه تند با قبلی ها برابر است. پس:
$ \widehat{O1} = \widehat{O2} = \widehat{O3} =60$
زوایای O4 ,O5, O6 به ترتیب با محاسبه 180-120=60 بدست می آیند.
مثلث COK بدلیل زض ز باقبلی ها برابر
مثلث های AOL و COL هم بنابر ض ز ض برابرند. پس زاویه L1=L2=90
پس :
$ \widehat{A1} = \widehat{A2} = \widehat{B1} = \widehat{B2} = \widehat{C1} = \widehat{C2} = \frac{180}{6} =30$
پس:
$ \widehat{A} = \widehat{B} = \widehat{C} =60$