در مثلث $ABC$ ، $AB=6 $ ،$BC=7$ و $AC=8 $ است. فاصله راس $B$ از $AD$، چند برابر فاصله راس $D$ از ضلع $AC$ خواهد بود

Question

در مثلث $ABC$ ، $AB=6 $ ،$BC=7$ و $AC=8$ است. نیمساز زاویه متوسط، ضلع روبه‌رو به زاویه را در $D$ قطع می کند. فاصله راس $B$ از $AD$، چند برابر فاصله راس $D$ از ضلع $AC$ خواهد بود؟

Comments

کلمه  «متوسط» در سوال به چه معنایی است؟

---

سلام
زاویه متوسط، زوایه‌ای در مثلث که از کوچکترین زاویه بزرگتر و از بزرگترین زاویه کوچکتر است.

---

پس چرا ضلع BC را معرفی کردید؟ نیمساز زاویه متوسط مطمئنا زاویه مقابل به ضلع متوسط یعنی BC می باشه پس نیاز نیست که BC را معرفی کنید. بهتر است در متن سوال یا  «متوسط» حذف کنید یا  « BC» چون هر کدام دیگری نتیجه می دهد.
توجه کنید در صورت حذفBC باید  « ضلع مقابل» اضافه کرد.

---

با سلام
 چه بگوییم نیمساز زاویه متوسط ، چه بگوییم نیمساز زاویه A تفاوتی ندارد و ایرادی بر سوال وارد نیست. می‌توان گزینه هایی را که فرمودید برای سوال استفاده کرد، اما خود سوالی که نوشته‌ام ایرادی ندارد پس لزومی بر ویرایش سوال نیست. اما به خاطر توجه شما متن سوال تغییر میدهم

Answer 1

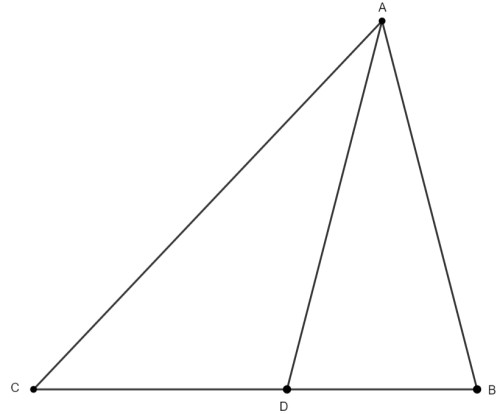
طبق قضیه نیمسازها $BC=3,3=CD=4$ و $AD=6 $ است.

$$S_{ABD}= \frac{1}{2}AD.BD sin(D_1) , S_{ACD}= \frac{1}{2}AD.CD sin(D_2) , sin(D_1)=sin(D_2) \Longrightarrow \frac{S_{ABD}}{ S_{ACD}}= \frac{3}{4} $$

اگر ارتفاع وارد بر $AD$ از راس $C$ را $BH_1$ , ارتفاع وارد بر $AC$ از راس $D$ را $DH_2$ در نظر بگیریم: $$S_{ABD}= \frac{1}{2}AD.BH_1$$ $$ S_{ACD}= \frac{1}{2}AC.DH_2 $$ آنگاه:

$$ \frac{S_{ABD}}{S_{ACD}}= \frac{6BH_1}{8DH_2} = \frac{3}{4} $$

در نتیجه: $$ \frac{BH_1}{DH_2}=1$$

Answer 2

1. با توجه به قضیه نیمساز ها، به راحتی می توان نتیجه گرفت که $BD=3, CD=4$ است.اندازه پاره خط $AD$ با استفاده از رابطه زیر برابر است با: $$AD^{2}=AB.AC-BD.CD \Longrightarrow AD=6 $$

   2. با استفاده از قضیه هرون مساحت مثلث های $ABD,ACD$ به ترتیب برابر $\frac{9 \sqrt{15} }{4},3 \sqrt{15} $ است.

   3. ارتفاع وارد بر $AD,AC$ را به ترتیب $BH',DH$ می نامیم و با توجه به مورد 2 که ذکر شد: $$BH'=DH= \frac{3 \sqrt{15} }{4} $$ در نتیجه: $$ \frac{BH'}{DH}=1 $$

Answer 3

باتوجه به قضیه نیمسازها $ \frac{AC}{AB}= \frac{CD}{BD} \Rightarrow \frac{3}{4}= \frac{CD}{BD} \Rightarrow \frac{3}{7}= \frac{CD}{7} \Rightarrow CD=3,BD=4 $

مثلث های ADM و ABN به حالت داشتن دو زاویه مساوی متشابهند .

$ \frac{BN}{DM}= \frac{AB}{AD} $(*)

چون نقطه $D$ روی نیمساز است پس $DM=DI=x$ و $ y=AM=AI$ در مثلث های $DMC , DBI$

$ x^{2}= 9-(6-y)^{2}=16-(8-y)^{2} \Rightarrow y= \frac{21}{4} \Rightarrow x= \frac{3 \sqrt{15} }{4} $

$AD= \sqrt{ x^2+y^2 }=6 $

$$ \frac{BN}{DM}= \frac{4}{3} \Rightarrow \color{red}{BN=\frac{4}{3} DM} $$

Comments

بنظرم راه حل @good4us درسته.

---

good4us@
مثلثی که رسم کردید طبق فرضیات درست اسم گذاری نشده است به همین دلیل است که پاسختان درست نیست. اما راه حلتان بسیار زیباست. ممنون می شوم که راه حلتان را ویرایش کنید.

---

Dana_Sotoudeh@ نام مثلثی که اشتباه بود تصحیح شد متشکرم

---

@good4us
با سلام خدمت شما
مثلثی که در پاسختون رسم کردید، با فرض سوال مطابقت ندارد. علاوه بر آن جواب سوال سه چهارم نمی شود بلکه جواب برابر ۱ است.

---

Dana_Sotoudeh@ نام های رئوس B و C را جابجا قرار دادم . البته این خود یک سوال جالب هم شد که این دو فاصله از نسبت 4 به 3 مانند دو ضلع مثلث برخوردار می شود .