این سوال به وسیله قضایای هندسه ۲ دبیرستان قسمت دایرهها به راحتی قابل حل است.
اولا طبق قضیه هندسه ۲، چهارضلعی که زوایای روبروش مکمل هم باشند را میتوان در یک دایره محاط کرد. حال چون زاویهٔ $EDA$ و $B$ هر کدام $90$ درجه هستند پس مکملاند. زاویههای $A$ و $BED$ هم مکملاند پس چهارضلعی $ABED$ در یک دایره محاط میشود.
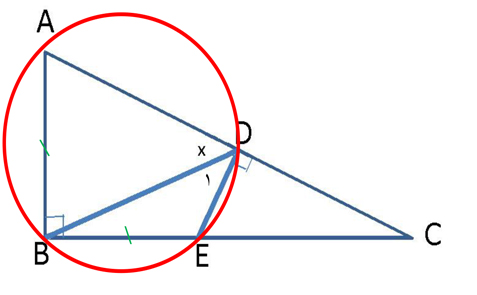
طبق هندسه ۲، میدانیم که کمانهای روبرو به دو وترِ برابر، باهم مساوی هستند. پس
$$
AB=BE\Longrightarrow\overset{\frown}{AB} =\overset{\frown}{BE}
$$
همچنین میدانیم که زاویهٔ $BDA$ با زاویهٔ $D_1$ برابر است چون هر دو زاویههایی هستند که روبروی کمانهای برابری قرار گرفتهاند. پس $\hat{D}_1=x$. از طرفی $x+\hat{D}_1=90$. بنابراین $x=45$.