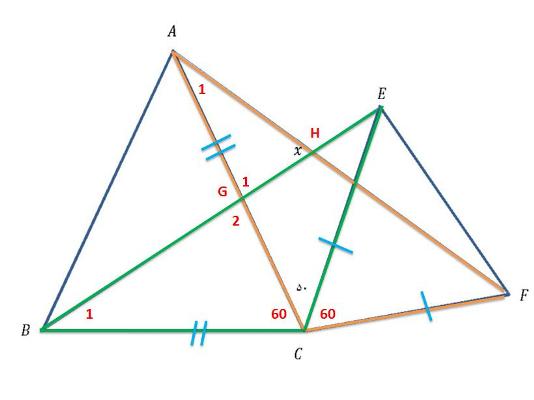
برای حل کافیست دو مثلث مشخص شده رو در نظر بگیریم که به حالت ض زض همنهشت هستند لذا $ \widehat{A} _{1} = \widehat{B} _{1} $
میدانیم $ \widehat{G} _{1} = \widehat{G} _{2} $ چون متقابل به راس هستند لذا اگر برای دو مثلث $ AGH$ و $ BGC $ مجموع زوایا را بنویسیم داریم:
$$ \begin{cases} \widehat{A} _{1} +x+ \widehat{G} _{1} =180\\ \widehat{B} _{1} +60+ \widehat{G} _{2} =180\end{cases} $$
لذا داریم $ x=60 $