Ш§ШЁШӘШҜШ§ Щ…ЫҢШ§ЩҶЩҮ ЩҮШ§ЫҢ ШҜЩҲ ШіШ§ЩӮ ШұШ§ ШЁЩҮ ЩҮЩ… ЩҲШөЩ„ Щ…ЫҢЪ©ЩҶЫҢЩ… ЩҲ ЫҢЪ©ЫҢ Ш§ШІ ЩӮШ·ШұЩҮШ§ ШұШ§ ШЁЩҮ ШҜЩ„Ш®ЩҲШ§ЩҮ ШұШіЩ… Щ…ЫҢ Ъ©ЩҶЫҢЩ… ЩҒШұШ¶ Ъ©ЩҶЫҢШҜ Щ…ШӯЩ„ ШЁШұШ®ЩҲШұШҜ Ш§ЫҢЩҶ ШҜЩҲ $o$ ШЁШ§ШҙШҜ . ЪҶЩҲЩҶ Щ…ЫҢШ§ЩҶЩҮ ШЁШ§ ШҜЩҲ ЩӮШ§Ш№ШҜЩҮ Щ…ЩҲШ§ШІЫҢ Ш§ШіШӘ Щ„Ш°Ш§ ШҜШұ Щ…Ш«Щ„Ш« Щ…Ш№Щ„ЩҲЩ… ШҙШҜЩҮ
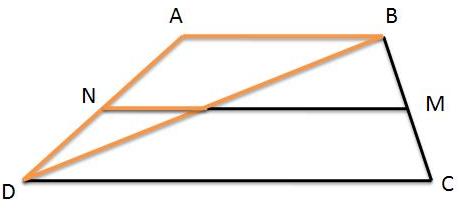
Ш§ЪҜШұ ЩӮШ¶ЫҢЩҮ ШӘШ§Щ„Ші ШұШ§ ШЁЩҶЩҲЫҢШіЫҢЩ… ШҜШ§ШұЫҢЩ…:
$$ 1= \frac{DN}{NA} = \frac{DO}{OB} \Rightarrow Do=OB$$
ШӯШ§Щ„ Ш§ЪҜШұ ЩӮШ·Шұ ШҜЫҢЪҜШұ ЩҮЩ… Ш§ШІ Ш§ЫҢЩҶ ЩҶЩӮШ·ЩҮ ЫҢШ№ЩҶЫҢ $o$ Ш№ШЁЩҲШұ Ъ©ЩҶШҜ ШЁЩҮ Ш·ЩҲШұ Щ…ШҙШ§ШЁЩҮ ЩҶШӘЫҢШ¬ЩҮ Щ…ЫҢ ШҙЩҲШҜ ЩӮШ·Шұ ЩҶШөЩҒ Щ…ЫҢ ШҙЩҲШҜ. Ш§Щ…Ш§ Щ…ЫҢ ШҜШ§ЩҶЫҢЩ… Ъ©ЩҮ Ш§ЪҜШұ ШҜШұ ЫҢЪ© ЪҶЩҮШ§ШұШ¶Щ„Ш№ЫҢ ЩӮШ·ШұЩҮШ§ ЫҢЪ©ШҜЫҢЪҜШұ ШұШ§ ЩҶШөЩҒ Ъ©ЩҶЩҶШҜ ЪҶЩҮШ§ШұШ¶Щ„Ш№ЫҢ Щ…ШӘЩҲШ§ШІЫҢ Ш§Щ„Ш§Ш¶Щ„Ш§Ш№ Ш§ШіШӘ.(ШӘЩ…ШұЫҢЩҶ ШҜШұШі ЩҮЩҶШҜШіЩҮ 1)
ЩҫШі ШІЩ…Ш§ЩҶЫҢЩ…ШӯЩ„ ШЁШұШ®ЩҲШұШҜ ШҜЩҲ ЩӮШ·Шұ ШұЩҲЫҢ Ш§ЫҢЩҶ Ш®Ш· ЩӮШұШ§Шұ Щ…ЫҢЪҜЫҢШұШҜ Ъ©ЩҮ Щ…ШӘЩҲШ§ШІЫҢ Ш§Щ„Ш§Ш¶Щ„Ш§Ш№ ШҜШ§ШҙШӘЩҮ ШЁШ§ШҙЫҢЩ….