همان طور که می دانید بردار ها در فضای دوبعدی دارای دو مولفه ی x و y هستند. و منظور از جمع برداری آن ها این است که مقدار مولفه ی xهر بردار با مقدار مولفه ی x بردار دیگر با هم جمع شود و مقدار مولفه ی y هر بردار هم با مقدار مولفه ی y بردار دیگر با هم جمع شود. بنابراین برای جمع دو بردار آن ها را در امتداد هم قرار می دهند و بردار حاصل جمع آن ها برابر برداری است که ابتدای آن ابتدای بردار اول و انتهای آن ، انتهای بردار دوم می باشد(روش مثلثی). و شبیه این است که دو بردار ابتدایی دو ضلع کنار هم متوازی الاضلاع هستند و بردار برآیند قطر آن می باشد.( می توان دو ضلع دیگر متوازی الاضلاع را با کشیدن دو خط که هم طول و موازی دو بردار اولیه هستند رسم نمود)
از آن جایی که در متوازی الاضلاع ضلع های روبرو با هم موازی و برابر هستند، می توان برای جمع دو بردار به جای این که دو بردار را در راستای هم قرار داد، آن ها را طوری رسم نمود که ابتدای آن ها در یک نقطه باشد. در این صورت برای به دست آوردن بردار برآیند دو ضلع دیگر متوازی الاضلاع را رسم کرده و قطر متوازی الاضلاع همان بردار برآیند است. این حالت هم مانند حالت قبل است با این تفاوت که بردار های اولیه دو ضلع دیگر متوازی الاضلاع هستند. در واقع در این حالت روش تغییر نکرده و فقط جای بردار را کمی جابجا نموده ایم.
اگر در هر دو حالت بردارهای اولیه و برآیند آن ها در یک صفحه ی مختصات رسم شود به طور واضح دیده می شود که مولفه ی x بردار برآیند با مجموع مولفه ی x دو بردار اول و مقدار مولفه ی y آن برابرمجموع مولفه ی y دو بردار اول است.
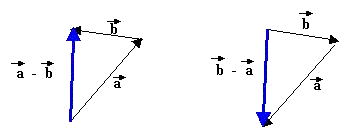
به همین ترتیب برای تفریق بردارها ازيك نقطه برداري مساوي و موازي برداري كه مثبت است رسم كرده ؛ سپس به دنبال آن برداري متناظرو موازي با بردار منفي ولي در خلاف جهت آن رسم مي كنيم . سپس از بردار مثبت به منفي وصل مي نماييم و مانند حالت قبلی بردار برآیند را به دست می آوریم.
همچنین اگر قرار باشد یک عدد در یک بردار ضرب شود، یعنی برداری چند برابر شود، آن عدد هم در طول و هم در عرضش ضرب می شود. چون هم در طول و هم در عرض ضرب می شود، نسبت طول و عرض نسبت به هم تغییری نمی کند در نتیجه راستای بردار تغییر نمی کند یعنی بردارهای همگی با هم موازی هستند.
برگرفته شده از akramdowlatabadi.blog.ir و سایت تبیان