جواب برابر است با $\,4+5+7=16\,$.
مسأله را در حالت کلی تری در نظر می گیریم. فرض می کنیم خطی که اضلاع $AB$ و $BC$ از مستطیل $ABCD$ را قطع کرده است از رئوس $A$ ، $B$ و $C$ به ترتیب دارای فواصل $ d_{1} $ ، $ d_{2} $ و $ d_{3} $ می باشد. با توجه به شکل زیر فرض می کنیم خط $\,l\,$ اضلاع $AB$ و $BC$ را به ترتیب در $M$ و $N$ قطع می کند.
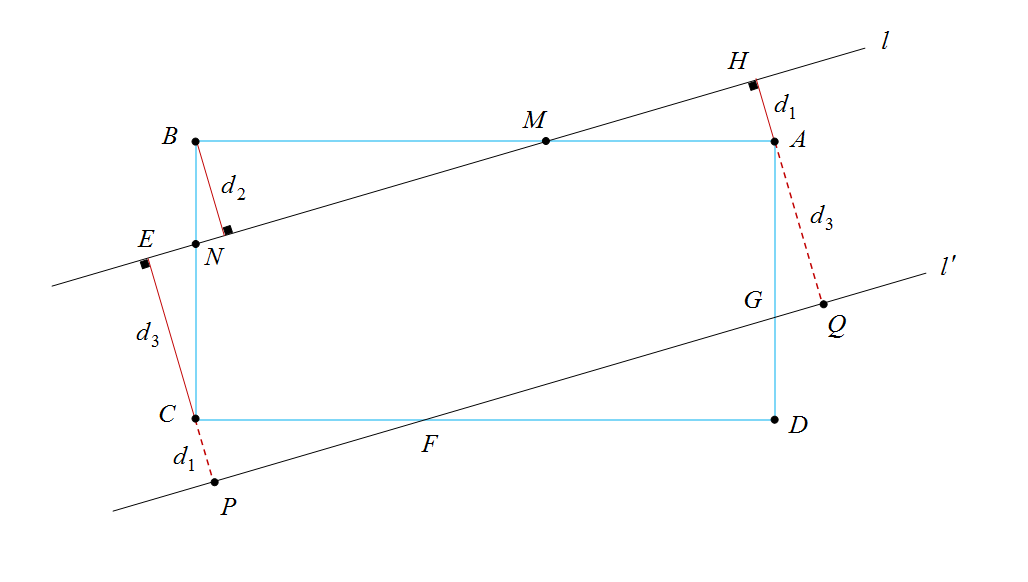پاره خط $EC$ را از نقطه $C$ به اندازه $ d_{1} $ امتداد داده و رأس حاصل را $P$ و پاره خط $HA$ را از نقطه $A$ به اندازه $ d_{3} $ امتداد می دهیم و رأس حاصل را $Q$ می نامیم. خطی را گذرا از نقاط $P$ و $Q$ رسم می کنیم و آن را $ l' $ می نامیم. واضح است که $ l \parallel l' $ . از آن جا که $ABCD$ و $HEPQ$ مستطیل هستند ($\,\,EH \parallel PQ\,\,$،$\,\,EP \parallel HQ\,\,$،$\,\,BC \parallel AD\,\,$و$\,\,BA \parallel CD\,\,$) پس با توجه به تساوی زوایای هم ارز، مثلثهای $CEN$ و $AQG$ و همچنین مثلث های $CPF$ و $AHM$ با هم متشابه هستند و چون $\,\,CP=AH\,\,$ و $\,\,CE=AQ\,\,$ پس:
$$ CEN \cong AQG\,\,\,\,و\,\,\,\,AHM \cong CPF $$
بنابراین $NM=FG$ . با توجه به توازی اضلاع مثلث های $BNM$ و $DGF$ تشابه و در نتیجه همنهشتی آن ها واضح است پس ارتفاع های وارد بر وتر ها در این دو مثلث با هم برابرند بنابراین اگر فاصله نقطه $D$ از خط $l$ ، $ d_{4} $ باشد آنگاه:
$$ d_{4} = d_{1} + d_{2} + d_{3} $$
هر چند که مسأله چندان ساده نبود که حل آن فوراً حاصل شود اماّ طراحی آن بسی شگفت انگیز است. به نظر من این گونه مسائل در طی یک سری مشاهدات و از طریق تجربه طراحی می شوند و نکات وسیعتری در آن ها یافت خواهد شد.
