یک چهار وجهی منتظم در واقع هرمی است که هر وجه آن مثلث متساوی الاضلاع است همانگونه که در شکل زیر مشاهده می کنید :
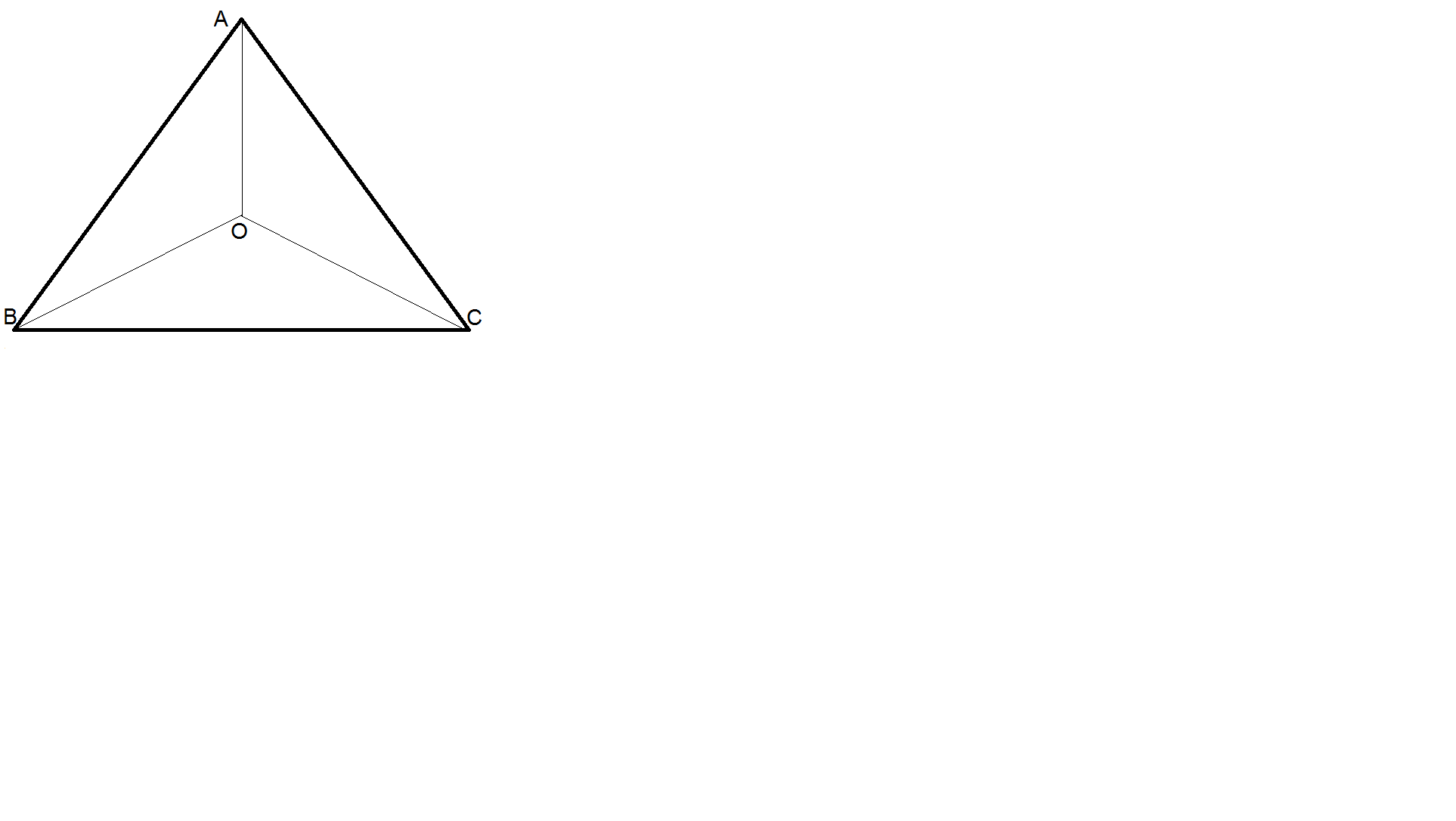
حال فرض کنید طول هر ضلع آن $a$ است . ابتدا به سه نکته زیر توجه نمایید :
$1$ : حجم هرم که مساحت قاعده آن $S$ و ارتفاع آن $h$ است برابر است با :
$$V=\frac{1}{3}Sh$$
$2$ : مساحت مثلث متساوی الاضلاعی که طول ضلع آن $a$ است برابر است با :
$$S=\frac{\sqrt{3}}{4}a^2$$
$3$ : در مثلث $ABC$ که طول اضلاع آن $a,b,c $ است داریم :
$$a^2=b^2+c^2-2ab\ cos \hat{A} $$
$$b^2=a^2+c^2-2ab\ cos \hat{B}$$
$$ c^2=a^2+b^2-2ab\ cos \hat{C} $$
حال حجم چهر وجهی منتظم را بدست می آوریم . توجه داشته باشیم که قاعده چهر وجهی منتظم یک مثلث متساوی الاضلاع به طول ضلع $a$ است پس مساحت قاعده آن برابر است با $ \frac{\sqrt{3}}{4}a^2$ پس برای محاسبه حجم چهار وجهی منتظم کافی است ارتفاع آن را بدست آوریم
ارتفاع رسم شده از راس $A$ را که بر قاعده $OBC$ فرود می آید را در نظر می گیریم و فرض کنیم پای عمود نقطه $H$ است . به شکل زیر توجه کنید :
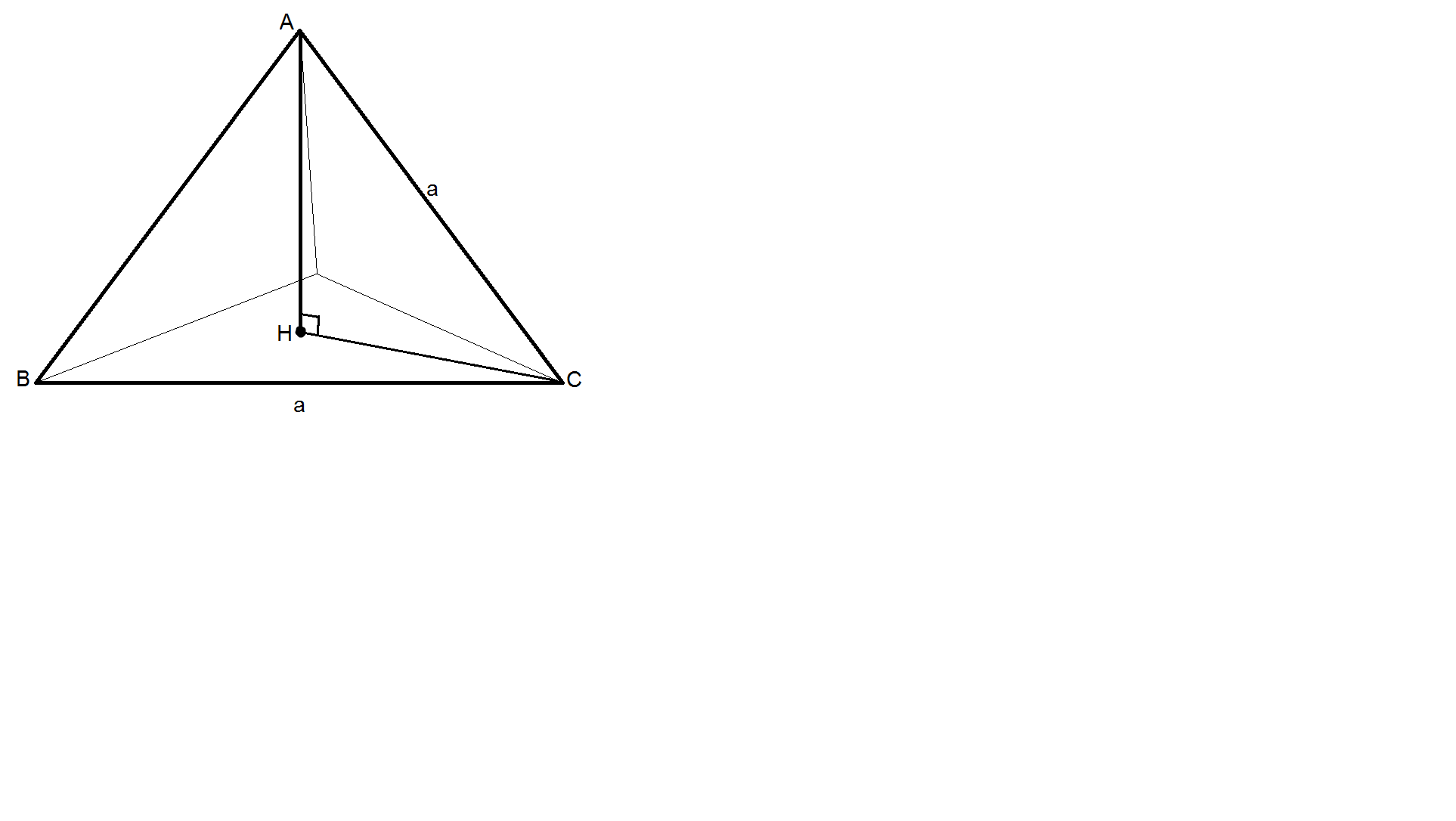
نقطه $H$ مرکز مثلث متساوی الاضلاع $OBC$ است . ابتدا طول پاره خط $HC$ را بدست می آوریم . به شکل زیر توجه کنید :
فرض کنید $HC = OH = b$ طبق نکته $3$ داریم :
$$a^2=b^2+b^2-2b^2cos120$$
$$ \Rightarrow b=\frac{\sqrt{3}}{3}a$$
پس $HC = \frac{\sqrt{3}}{3}a$ . حال طبق قضیه فیثاغورث داریم :
$$AH^2+HC^2=a^2$$
$$ \Rightarrow AH^2=a^2-(\frac{\sqrt{3}}{3}a)^2$$
$$ \Rightarrow AH=\frac{\sqrt{2}}{\sqrt{3}}a$$
بنابراین حجم چهار وجهی منتظم برابر است با :
$$V=\frac{1}{3}(\frac{\sqrt{3}}{4}a^2)(\frac{\sqrt{2}}{\sqrt{3}}a)=\frac{\sqrt{2}}{12}a^3$$
