محیط اجسام هندسی

Question

سلام. محیط شکل های کره و استوانه و مخروط رو میخواستم بدونم.

Answer 1

محیط معمولا برای شکل‌های دوبعدی تعریف می‌شود و برای شکل‌های سه بعدی مثل کره و استوانه و مخروط معمولا مساحت جانبی رو در نظر می‌گیرند. البته اگر این شکل‌های سه بعدی را با یک صفحه قطع دهیم در اینصورت شکل دوبعدی حاصل می‌شود که می‌توان محیط آن را حساب کرد و در این حالت دایره هایی با شعاع‌های نابرابر به دست می‌آید که می‌توان محیط دایره با بزرگترین شعاع را محیط کره در نظر گرفت. پس می توان گفت که محیط کره به شعاع $ R $ برابر است با $ 2\pi R$ یعنی محیط دایره‌ی عظیمه! همچنین برای استوانه و مخروط فرمولی برای محیط وجود ندارد ولی به آنها محیط دایره را نسبت می‌دهیم. با این حال توجه کنید که ما برای اشکال سه بعدی محیط را تعریف نمی‌کنیم مگر اینکه با توجه به توضیحات بالا خودمان قرارداد کنیم که منظور از محیط اشکال سه بعدی محیط بزرگترین سطح مقطع است.

در زیر فرمول مساحت(جانبی) این اشکال را می‌نویسم که ممکن است مدنظر شما بوده باشد:

$ =4\pi R^2$ مساحت کره به شعاع $R$

$=2\pi Rh $ مساحت جانبی استوانه به شعاع $R$و ارتفاع $h$. توجه کنید که اگر بخواهید مساحت کل استوانه را بیابید باید مساحت رو تا قاعده‌ی استوانه را به مساحت جانبی اضافه کنید. یعنی مساحت کل استوانه برابر است با $ 2\pi R h+2\pi R^2 $

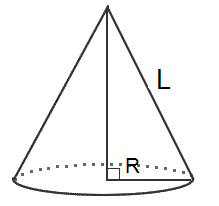
$ =\pi R^2+\pi R L$ مساحت کل مخروط به شعاع $R$ و $ L$ طول یال جانبی مخروط است.

اگر باز مشکلی هست دیدگاه بذارید.

Comments

ممنون از جوابتون.
ولی من هنوز برام مبهمه. اگه همین شکلای سه بعدی رو بازشون کنیم میشن یه شکل دوبعدی.
مثلا مکعب رو باز کنیم شکلش به وضوح معلوم میشه که میتونیم محیطش(دور تا دورشو )محاسبه کنیم.

---

خواهش می‌کنم. ممنون از سوال خوبتون.
خوب این تعریفی که شما از محیط یک شکل سه بعدی ارایه کردید باز هم چیزیه که شما قرارداد کردید ممکن است کس دیگه تعریف دیگه‌ای بگه. ولی واقعا تعریف خاصی برای محیط اشکال سه بعدی وجود ندارد. با این حال همونطور که گفتم بعضی وقت‌ها مناسب به نظر می‌رسه که به کره، استوانه و مخروط به شعاع $R$ مقدار $2\pi R$ را به عنوان محیط نسبت می‌دهند که منظور از آن محیط بزرگترین سطح مقطع حاصل است.

---

سلام دوست عزیز اگه قراره اینطوری تفسیز کنی ....باید بگی اگه مثلا با یه نخ دومتری یه دایره درست کنیم محیط دایره میشه همون دومتر؟؟؟؟؟؟ در حالی که محیط این دایره جور دیگه محاسبه میشه؟؟؟؟؟

---

متوجه نمیشم. خوب اگه با یک نخ دومتری یک دایره بسازیم محیط دایره دقیقا همون دو متر میشه دیگه. ولی سوال ایشون در مورد کره است.

---

سلام به شما دوست عزیز و همه دوستان ریاضی دوست ...خوب و با دقت لطفا دیدگاه من رو مطالعه داشته باشید ، مفهوم محیط یعنی دور تا دور یک شکل .حالا چه زمانی میتونیم دور تا دور یک شکل رو حساب کنیم ؟ زمانی که اون شکل پایانی داشته باشه ! متوجه میشید ؟ یعنی اینکه الان مربع در اخر ضلع و راسش به پایان میرسد و از انجا به بعد به هیچ نقطه دیگه ای متصل نیست پس برای بدست اوردن محیط مربع کافی است که این نقاط را در نظر بگیریم ...حالا این به پایان رسیدن فقط برای اشکال دو بعدی هست یعنی اینکه شکلی که شما روی کاغذ میکشید چون پر حالت طبیعی چیزی به نام دو بعدی نداریم چون که نباید هیچ قطری داشته باشه و درواقع باید قطرش برابر صفر باشه که عملا غیر ممکنه . اما در اشکال سه بعدی به دلیل اینکه اشکال پایانی ندارند و بعد از پایان هر ضلع به ضلع دیگری در مجه متفاوت متصل میشوند ، درواقع پایانی ندارند و به همین دلیل هم نمیتوان براشون محیطی تعریف کرد ...البته این درصورتی درسته که منظور شما از محیط واقعا محیط باشه نه اینکه محیط رو جایگزین واژه ی دیگه ای مثل سطح مقطع کرده باشید ....شاد و پیروز باشید !!! بدرود

Answer 2

محیط شکل های هندسی کره، استوانه و مخروط به معنای فضایی است که این اشکال در آن قرار گرفته‌اند. به عبارت دیگر، محیط شامل فضای سه بعدی است که شکل های هندسی مذکور در آن قرار دارند. این مفهوم در مباحث هندسه فضایی و هندسه تحلیلی مورد استفاده قرار می‌گیرد.

محیط کره بزرگترین مقطع دایره ای که می توانیم از یک کره برش دهیم تعریف کرد. فرمول محیط یک کره با شعاع $r$ برابر$$2πr$$ است.

در مورد استوانه، با ایجاد یک مقطع عمودی در امتداد خط، به موازات ارتفاع آن، می توانیم محیط را پیدا کنیم، برابر است با $$2d+2h$$ که $d$ قطر استوانه و $h$ ارتفاع آن است.