پاسخ برای نسخهای از پرسش که پیش از ویرایش نوشتهبودید
پیش از ویرایش پرسش شما به این معنا بود که یک جورسازی با دقیقا $\frac{m}{\Delta}$ یال وجود خواهد داشت. در این حالت:
به راحتی میتوانید مثال نقض بسازید. گراف ۶ گرهای، ۵ یالی زیر را در نظر بگیرید. این گراف دوبخشی نیز است. آشکارا هر جورسازیای از آن دارای ۱ یا ۲ یا ۳ یال است. درجهٔ بیشنه برابر ۳ است. اما $\frac{5}{3}=1\frac{2}{3}$.
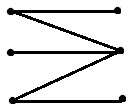
پاسخ برای نسخهٔ پس از ویرایش پرسش
در این نسخه، پرسش به این معنا است که یک جورسازی با دستکم $[\frac{m}{\Delta}]$ یال (که کروشه برای جزءصحیح به کار رفتهاست) وجود دارد. در این حالت:
قضیهٔ Konig را به یاد آورید (یا اگر نمیدانید آن را پیدا و بخوانید برای نمونه در این صفحهٔ ویکیپدیا آمدهاست - اینجا کلیک کنید -). این قضیه بیان میکند که تعداد یالهای حاضر در یک جورسازی بیشینه برای یک گراف دوبخشی دلخواه برابر است با تعداد گرههای یک پوشش کمینه. فرض کنید $K$ یک پوشش کمینه برای گراف دوبخشیتان باشد. چون هر یالی باید دستکم یک سرش در $K$ باشد پس داریم $\sum_{v\in K}\deg (v)\geq m$. از طرفی درجهٔ هر گره چه داخل $K$ چه بیرون، از $\Delta$ کمتر یا مساوی است. پس داریم.
$$\begin{align}
& |K|m=\sum_{v\in K}\Delta\geq\sum_{v\in K}\deg (v)\geq m\\
& \Longrightarrow |K|\geq\frac{m}{\Delta}
\end{align}$$
که منظور از $|K|$ تعداد اعضای مجموعهٔ $K$ است. پس نه تنها ثابت کردیم که دستکم یک جورسازی با دستکم $[\frac{m}{\Delta}]$ تا یال وجود دارد، بلکه ثابت کردیم که به جای جزء صحیح (یعنی بزرگترین عدد صحیح کوچکتر از داخل جزءصحیح) میتوان عدد داخل جزءصحیح را به سمت بالا گرد کرد و جورسازی با این تعداد یال وجود دارد. و نه تنها این، بلکه کران پائینی برای تعداد یالهای جورسازی بیشینه هم پیدا کردم. اکنون به همان مثال پیشین نگاه کنید. چون گردکردن به سمت بالای $\frac{5}{3}$ عدد ۲ را میدهد پس مطمئن میشویم که جورسازی بیشینه حداقل ۲ یال دارد و هر جورسازی بیشینهای نیز یک مثال از جورسازیِ خواستهشده در پرسش میشود.