گراف مکعبی $Q_k$ برای عدد طبیعی $k$ که اشاره کردید گرافی با $2^k$ گره است که متناظر به اعضای مجموعهٔ $\lbrace 0,1\rbrace ^k$ یعنی مجموعهٔ $k$-تاییهای مرتب با درایههای صفر و یک (که میتوانید به عنوان نقاطی در فضای $k$-بعدی با مختصهای صفر و یک نیز در نظر بگیرید) است. و دو گره با یکدیگر همسایه هستند (بینشان یال است) اگر و تنها اگر تنها یک مؤلفهٔ متفاوت داشته باشند. برای نمونه $Q_3$ را در زیر میبینید (شکلهای این پست با نرمافزار Mathematica کشیده شدهاند).
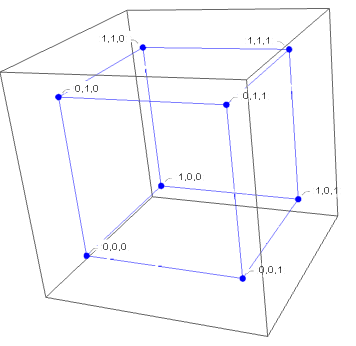
جورسازی یعنی انتخاب زوج گرهها به طوری که هر زوج گرهای با یک یال به هم وصل باشند و هیچ دو زوج گرهای اشتراک نداشتهباشند (به عبارت دیگر گرهای در دو زوجگره تکرار نشده باشد). یک جورسازی تام (کامل) است هر گاه هر گره در یک زوجگره گزیده شدهباشد. یعنی اجتماع این زوجها برابر با مجموعهٔ تمام گرههای گرافتان شوند.
بیاییم از $k$های گوچک شروع کنیم تا ببینیم آیا چیزی دستگیرمان میشود یا خیر. اگر $k=1$ آنگاه دو گره بیشتر نداریم که با یک یال به هم وصل هستند. خیلی بدیهی با جور کردن این دو گره با یکدیگر یک تک زوجگره داریم که یک جورسازی است و کامل هم هست. اگر $k=2$ جورسازی کامل همارز است با انتخاب دو ضلع (یال) موازی از مربعمان. اگر $k=3$ خیلی راحت از همان ایدهٔ یالهای موازی میتوانید شهودی ببینید که با انتخاب چهار بال موازی که با رنگ قرمز نشان دادهایم یک جورسازی کامل داریم.
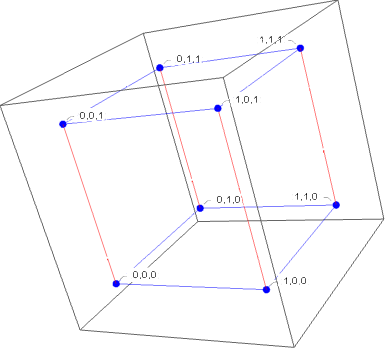
با نگاه کردن به مختصات گرههایی که با هم جور کردیم در این سه حالت خیلی راحت یک الگو میبینیم. یکی از محورها را به دلخواه انتخاب کنید، من آخرین محور را انتخاب میکنم پس در حالتهای $k=1,2,3$ به ترتیب محورهای $x$ سپس $y$ و در آخر $z$ را در نظر گرفتهام. ولی توجه کنید که انتخاب دست خودتان است. آنگاه توجه کنید که هر گره از گرافمان که برداریم دقیقا یک گرهٔ دیگر وجود دارد که همهٔ مؤلفههایش با مؤلفههای این گره برابر هستند غیر از مؤلفهٔ مربوط به محوری که انتخاب و ثابت گرفتهایم. پس یک یال بین این دو وجود دارد و میتوانم آن دو را با هم جور کنم. بعلاوه هر گره تنها در یک زوجگره با این ویژگی حضور دارد پس یک جورسازی داریم. و در نهایت چون شرطی که باعث شود فقط بعضی گرهها را انتخاب کنیم نگذاشتهایم پس تمام گرهها در جورسازی شرکت کردهاند و جورسازیمان کامل است. جورسازیمان $2^{k-1}$ زوجگره دارد.