چرا $\lim_{x\to 0}\frac{\sin x}{x}=1$ ؟

Question

دلیل حاصل عبارت $ \lim_{x \rightarrow 0} \frac{sin x}{x} $ چرا میشه $1 $ ؟

Answer 1

برای اینکه بفهمیم چرا حد $ \lim_{ \theta \rightarrow 0} \frac{\sin \theta}{\theta} $ میشه $1 $ ، قضیه مهم زیر رو در نظر میگیریم:

قضیه افشردگی : فرض کنید توابع $ f, g $ و $ h $ روی بازه ی $ I $ ی شامل $ a $ ، احتمالا بجز خود $ a $ ، تعریف شده باشند و به ازای هر $ x $ در $I $ که .$ x \neq a $ ، $ f(x) \leq g(x) \leq h(x) $ همچنین فرض کنید که هر دو حد توابع $f $ و $ h $ در $a $ موجود و برابر $l $ باشد، آنگاه $ \lim_{x \rightarrow a} g(x)=l $ است.

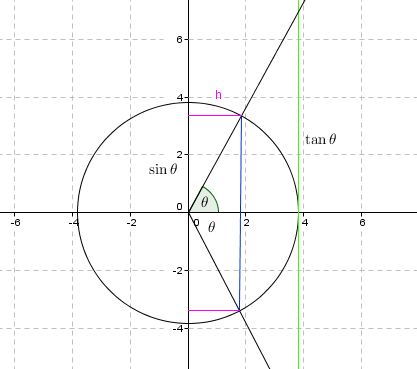
شکل بالا رو در نظر بگیرید. با توجه به اینکه $ \theta \neq 0 $ و $ | \theta | < \frac{\pi}{2} $ با مقایسه مساحت ها در شکل داریم: $$\sin \theta < \theta < \tan \theta\quad ,\theta > 0$$ $$\tan \theta < \theta < \sin \theta \quad ,\theta < 0 $$

بنابراین اگر $ \theta \neq 0 $ داریم $$ 1 < \frac{\theta}{\sin \theta} < \frac{1}{\cos \theta} $$ .

اما چون $ \cos \theta $ تابعی پیوسته است، لذا $ \lim_{\theta \rightarrow 0} \frac{1}{\cos \theta} =1 $. حد تابع ثابت $ 1 $ نیز، وقتی $ \theta$ به $ 0 $ میل میکنه برابر با
$1 $ هستش. چون $ \frac{\theta}{\sin \theta} $ بین $1 $ و $ \frac{1}{\cos \theta} $ قرار داره و هر دوی این توابع به $ 1 $ میل میکنن، تابع وسطی هم بنابر قضیه فشردگی، به $ 1 $ میل میکنه. یعنی $ \lim_{ \theta \rightarrow 0} \frac{\sin \theta}{\theta} $ . (وقتی حد $ \frac{f}{g} $ وقتی $ x $ به $ a $ میل کنه، وجود داشته باشه، حد $ \frac{g}{f} $ هم وجود داره و برابر معکوس حد $ f $ بر $ g $ هستش البته به شرطی که حد تک تک توابع $f , g $ در $a $ موجود باشن.) توجه میکنیم که $ \theta$ بر حسب رادیانه.

این اثبات کاملشه اما اگه بخوایم شهودی به قضیه نگاه کنیم، شکل این تابع در کتاب حسابان قدیم، وجود داره که میتونین بهش مراجعه کنین.

Comments

بسیار عالی بود و اگر بخواهیم نکته تستی این سوال را برای کنکوریها بازگو کنیم این است که: $sin x$ وقتی $x$ به سمت صفر میل میکند هم ارز $x$ است.

---

جواب ابن سوالو از متن کتاب ریاضی سوم تجربی هم میتونید کمک بگیرید.تاهمیشه دم دستتون باشه

---

افشردگی نه دوست عزیز
{فشردگی}

---

این قضیه به قضیه فشردگی، افشردگی، فشار و ساندویچ معروف است.
ضمنا در کتاب درسی حسابان از افشردگی استفاده شده.

---

اثبات این قضیه در کتب درسی حسابان ، حساب دیفرانسیل و انتگرال و همینطور در
ریاضیات 3 تجربی موجود است.

Answer 2

می توان $\sin$ این گونه نوشت $$ \sin x=x-\frac{x^3}{3!}+ \frac{x^5}{5!}-\frac{x^7}{7!}+...\\ \Rightarrow \frac{\sin x}{x}=1-\frac{x^2}{3!}+ \frac {x^4} {5!}-...\\ \lim_{x \rightarrow 0} \frac{\sin x}{x}=1 $$

Comments

@AmirHosein
این رو چجوری نوشته؟
آیا این بست تیلور است؟

Answer 3

$$ \lim_{x \to 0} \frac{\sin x}{x}=\lim_{x \to 0} \lim_{v \to 0}\frac{\sin (x+v)-\sin v}{x}\\ =\lim_{v \to 0} \lim_{x \to 0}\frac{\sin (x+v)-\sin v}{x}=\lim_{v \to 0}\sin'v=\lim_{v\ \to 0} \cos v=1 $$

Answer 4

$$ \lim_{n \rightarrow \infty } \frac{\text{perimeter of circle}}{\text{perimeter of polygon}}=1 $$ $$ \lim_{n \rightarrow \infty } \frac{2 \pi}{2n\sin( \frac{\pi}{n} )}=1 $$ $$ \lim_{n \rightarrow \infty} \frac{ \frac{\pi}{n} }{\sin \frac{\pi}{n} }=1 $$