هر دو ساختار دیفرانسیل پذیر روی $ S^1 $ هم ارز هستند.
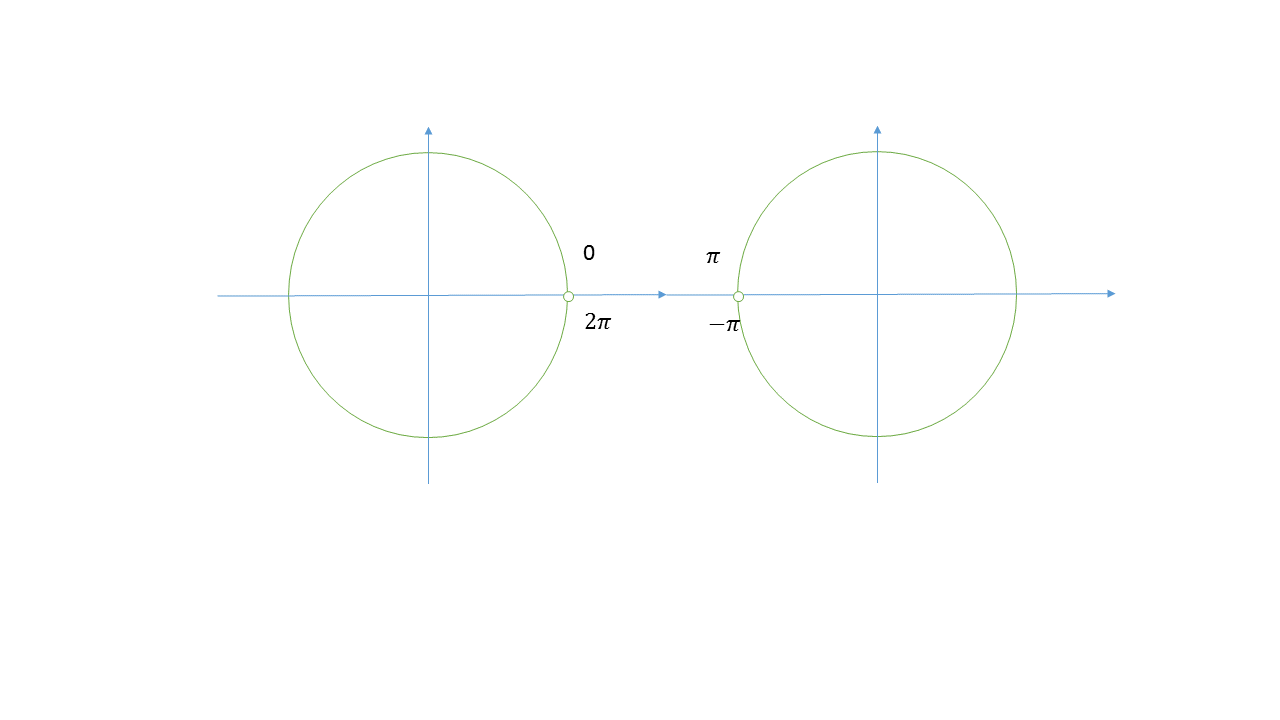
به عنوان مثال در پایین دو ساختار هم ارز تعریف شده اند. یک بار روی $ S^1 $ اطلس $ \mathcal A=\{x,x'\} $ که
$$ \begin{cases}x:\{(\cos\theta,\sin\theta):0< \theta< 2\pi\}\to(0,2\pi)\\(\cos\theta,\sin\theta)\mapsto \theta \end{cases}$$
و
$$ \begin{cases}x':\{(\cos\theta,\sin\theta):-\pi< \theta< \pi\}\to(-\pi,\pi)\\(\cos\theta,\sin\theta)\mapsto \theta \end{cases}$$
(خودتون میتونید ثابت کنید که واقعا اطلس هست)
حال اطلس $\mathcal A'=\{x_1,x_2,x_3,x_4\} $ را به صورت زیر در نظر بگیرید:
$$\begin{cases}x_1:\{(x,y)\in S^1: x > 0\}\to (-1,1)\\ (x,y)\mapsto y
\end{cases} $$
$$\begin{cases}x_2:\{(x,y)\in S^1: y > 0\}\to (-1,1)\\ (x,y)\mapsto x
\end{cases} $$
$$\begin{cases}x_3:\{(x,y)\in S^1: x < 0\}\to (-1,1)\\ (x,y)\mapsto y
\end{cases} $$
$$\begin{cases}x_4:\{(x,y)\in S^1: y< 0\}\to (-1,1)\\ (x,y)\mapsto x
\end{cases} $$
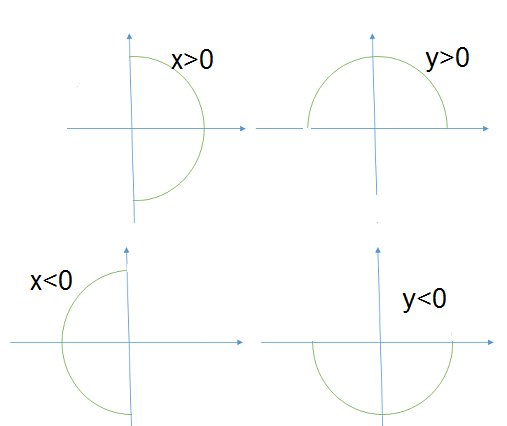
(خودتون ثابت کنید که این هم اطلس هست.)
در اینصورت $ \mathcal A $ و $ \mathcal A' $ هم ارز هستند یعنی $ \mathcal A\cup\mathcal A'$ هم یک اطلس است.(چرا؟)
