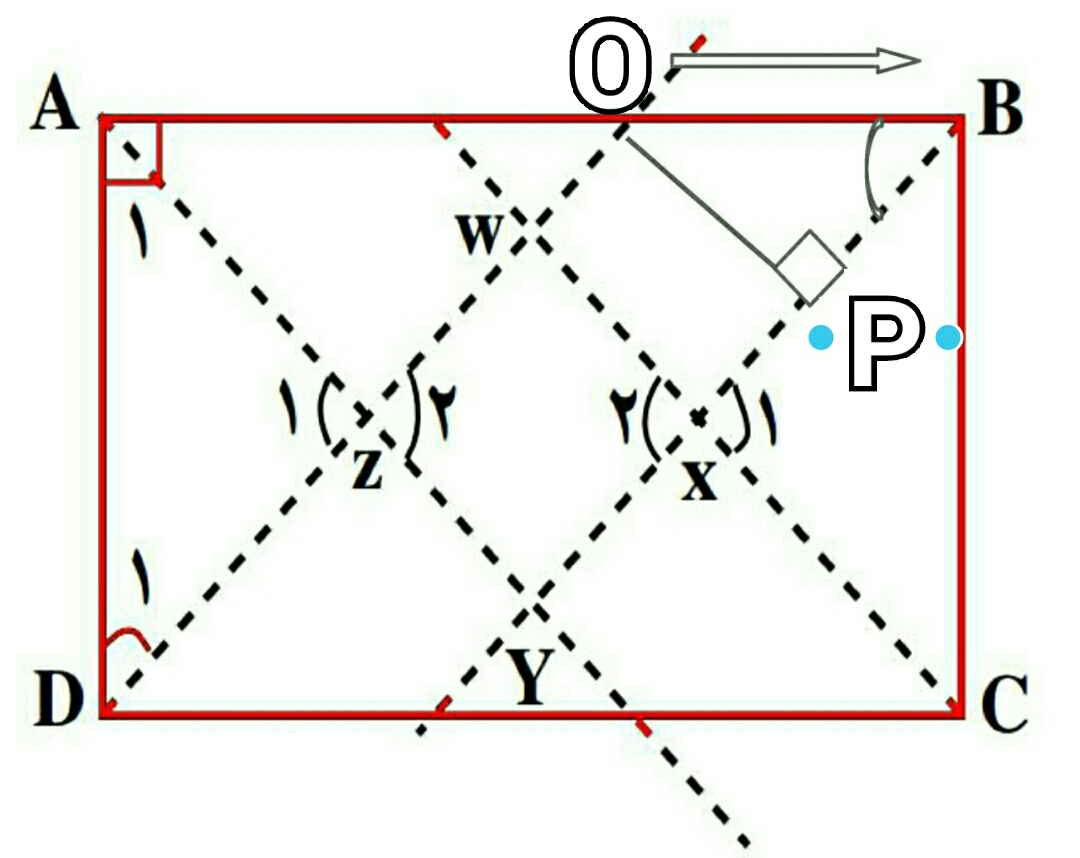
همه میدانیم،مستطیل هم نوعی متوازی الاضلاع است در شکل بالا میانه های همه رئوس رسم شده از نقطه o عمودی بر BXرسم میکنیم و پای عمود رو p مینامیم میدانیم op با wx برابر است و مثلث oBp متساوی الساقین است چون هردوزاویه پای ساق ۴۵ درجه با توجه به اینکه sin زوایه ۴۵ درجه برابر$ \frac{ \sqrt{2} }{2} $پس اندازه ضلع op رابدست می آوریم،اگر طول متوازی الاضلاع را M و عرض آن را N در نظر بگیریم اندازه وتر oB برای مثلثoBp میشود M-N پس اندازه ضلع op میشود
$ \frac{ \sqrt{2} }{2}(M-N) $
و از آنجا طول ضلع wx هم همین میشود و حال میتوان مساحت ۴ ضلعی داخلی تشکیل شده از میانه ها (که در اینجا مربع)
را نسبت به مساحت متوازی الاضلاع(که در اینجا مستطیل) بدست آورد