یک روش این است که برای مساحت از رابطه زیر استفاده میکنیم:
$$ S_{AMN}= S_{AMC} - S_{MNC} $$
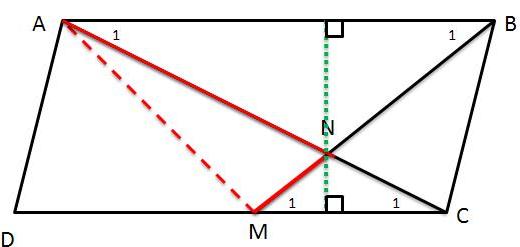
در شکل ارتفاع به طول $ h $ که ارتفاع متوازی الاضلاع است به رنگ سبز نمایش داده شده (از نقطه $N$ عبور میکند) اگر فرض کنیم طول قاعده برابر $a$ است مساحت متوازی الاضلاع برابر خواهد بود با $ah$
$$S_{AMC}= \frac{1}{2}h \times MC= \frac{1}{2}h \frac{a}{2} = \frac{ah}{4} $$
برای اینکه $ S_{MNC} $ را بدست آوریم کافیست دقت کنیم دو مثلث $ MNC $و $ANB$ به حالت دو زاویه متشابه هستند و نسبت تشابه برابر است با نسبت دو قاعده یعنی $ \frac{1}{2} $ پس نسبت ارتفاع ها هم برابر است با همین نسبت پس ارتفاع مثلث برابر است با $ \frac{h}{3} $
و لذا مساحت برابر است با :
$$S_{MNC} =\frac{1}{2} \times \frac{h}{3} \times MC= \frac{1}{2} \times \frac{h}{3} \times \frac{a}{2}= \frac{ah}{12} $$
لذا داریم:
$$ S_{AMN}= S_{AMC} - S_{MNC} = \frac{ah}{4}-\frac{ah}{12}= \frac{ah}{6} $$